ピタゴラスの定理の証明の代表例
このページにあるアニメーションのリスト（ハイパーテキストをクリックするとアニメーションがみられます。）
ここにもどるにはブラウザーの"Back" ボタンを使う。
目次
- 幾何学原論にあるユークリッドの証明
- ユークリッドの証明の変形 そのー1
- ユークリッドの証明の変形 そのー２
- Pappus of Alexandria による一般の三角形への拡張
- ピタゴラスによる証明
- 一般的 Dissection の考え方 ーーーー そのほかの巧妙な証明 ーーーー
- Leonardo Da Vinci の 証明
- Thâbit ibn Quarra の 証明
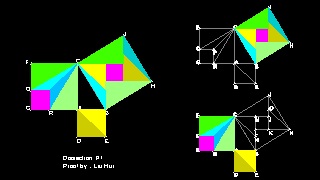
- Liu Hui の 証明
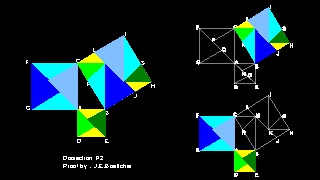
- J.E.Böttcher の 証明
ーーーー ピタゴラスの定理の一般化 ーーーー - ピタゴラスの定理の一般化ー平行四辺形への拡張
- De Gua の定理: ３ 次元への ピタゴラスの定理の拡張
- 球面座標での ピタゴラスの定理
幾何学の総ての定理の中で最も有名なものは ピタゴラスの定理 ( Pythagorean Theorem ) であると断言してもいい。 この名前は紀元前６世紀ごろギリシャにおける 数学を学ぶカルト的集団(いわゆる ピタゴラス学派) の中心的人物であった Pythagoras of Samos(多分 569-475 BC) に由来する。ピタゴラスの死後 約１５０年経って ユークリッド ( Euclid )(多分 ３２５-多分２６５ BC) が それまでの数学を体系立てて 書物にまとめ上げたのが 幾何学原論( The Elements ) である。 この本は人類の歴史上 聖書とならび 最も数多く出版されたものである。 この本がその後２０００年以上にわたって数学に与えた影響は測り知れない。
ピタゴラスの定理は ユークリッド の 幾何学原論 の第一巻の中で ４７番目の定理 として取り上げられている。
"直角三角形の直角をはさむ二辺の上の正方形の面積の和は 斜辺の上の正方形の面積に等しい。"
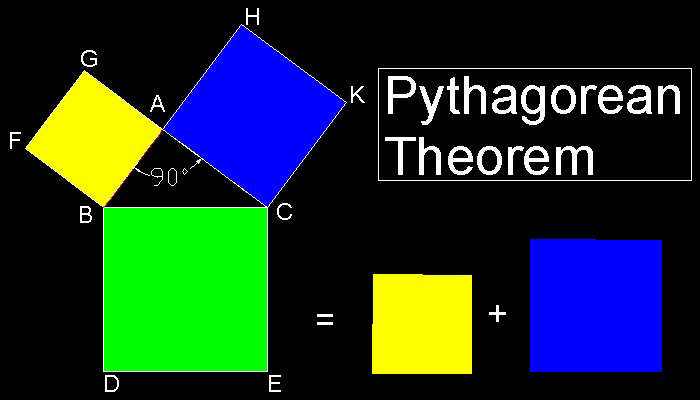
数学の定理の証明の数からいえば ピタゴラスの定理の証明が其の他の定理の証明に比べて圧倒的に多い。
Elisha Scott Loomis が 19２７ に発行した "ピタゴラスの定理" (原書名 The Pythagorean Proposition)(参考文献 １） には 何と 367 にも及ぶ 証明
が列記されている。
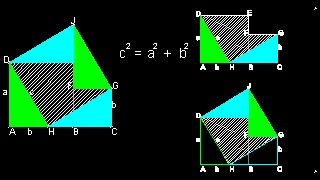
1. 幾何学原論にあるユークリッドの証明
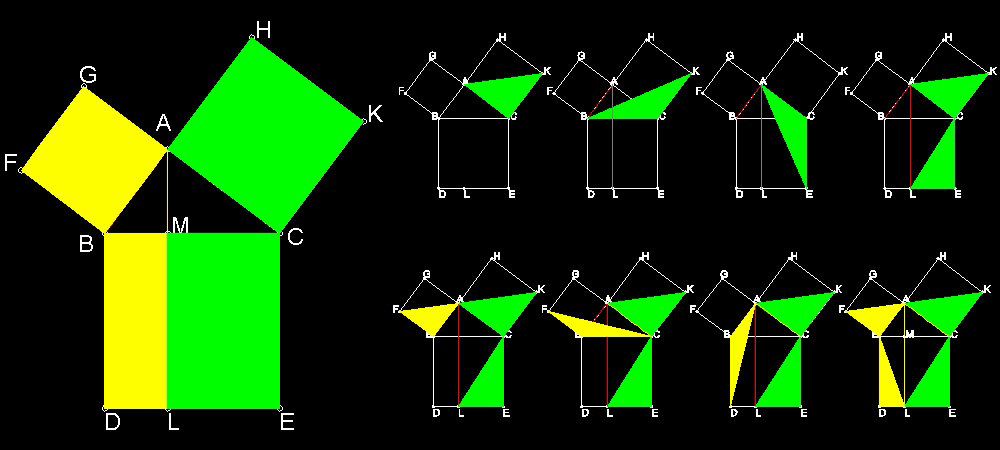
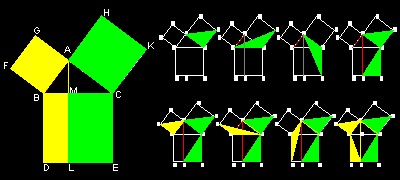
この証明は数多くの証明の中でも簡潔にして優美なものの一つである。 論理の進め方の中心は 緑の三角形 ACK, BCK, ACE そして 最後に MCE の面積が総て等しいということを示すことである。 それが正しければ 三角形 ACK, MCE の２倍の面積を持つ正方形 ACKH と 長方形 MLEC の面積が等しいことになる。 黄色のABFG と BDLM についても同様な議論から 其の面積が等しい ことがわかる。 従って、斜辺の正方形 CBDE の面積は直角を挟む二辺上の正方形 ABFG と ACKH の面積の和に等しい ということを証明したことになる。
この図面とアニメーションの作成方法 :
プログラム Euclid_47.lsp をロードする。 (load "Euclid_47")
コマンド ラインから Euclid_47_1 と実行命令をタイプする。
次の二つの証明は、三角形の代わりに 平行四辺形(長方形, 正方形を含む)、を扱うもので 証明 ＃１ の 変形と見ることができる。
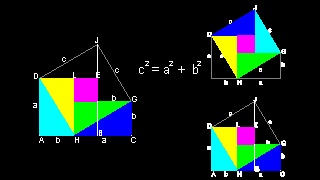
2. ユークリッドの証明（＃１）の変形 そのー1
Elisha Scott Loomis (参考文献 １．) の中では 幾何学的証明の ４２番目で Lecchio が １７５３年に公表したものである と述べられている。
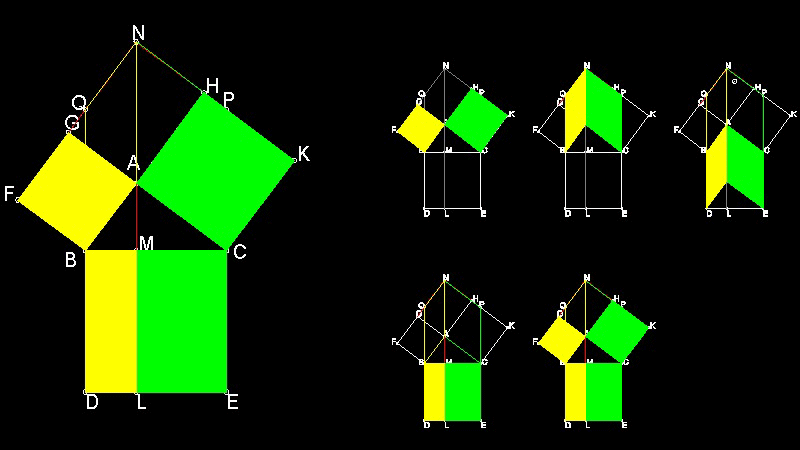
この図面とアニメーションの作成方法 :
プログラム Euclid_47.lsp をロードする。 (load "Euclid_47")
コマンド ラインから Euclid_47_3 と実行命令をタイプする。
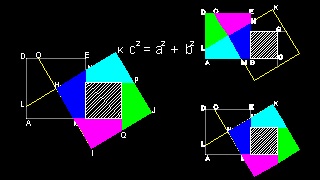
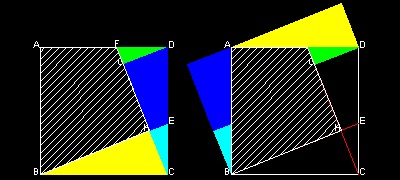
3. ユークリッドの証明（＃１）の変形 そのー2
B.F.Yanney が １９０３年 に 発表したものである。 (参考文献. 6) (p.283).
証明 #8 にも類似している。
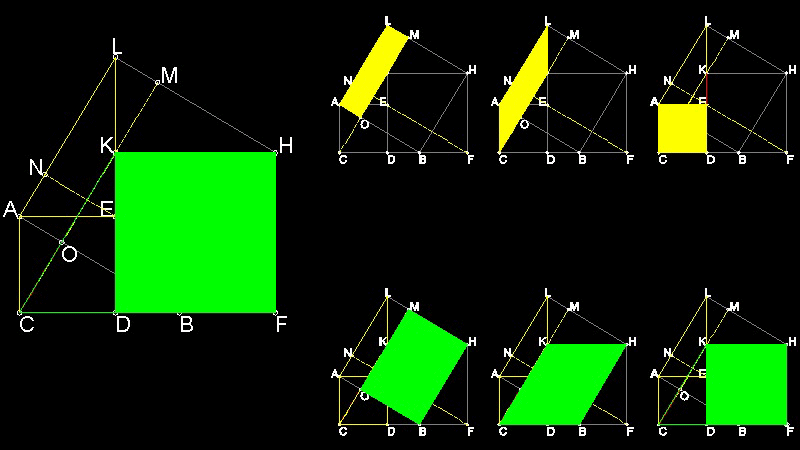
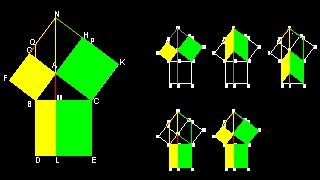
先ず CB = DF であるから 正方形 KHFD は CB上の正方形とみなせる。 次に LMOA,LKCA,ACDE の面積が等しいことを示す。 同様に MHBO、KHBC, KHFD の面積が 等しい。 従って 斜辺AB上の正方形 ABHL =LMOA + MHBO = ACDE + KHFD = AC上の正方形 +CB上の正方形
この図面とアニメーションの作成方法 :
プログラム Euclid_47.lsp をロードする。 (load "Euclid_47")
コマンド ラインから Euclid_47_9 と実行命令をタイプする。
4. Pappus of Alexandria による一般の三角形への拡張 (参考文献 3)
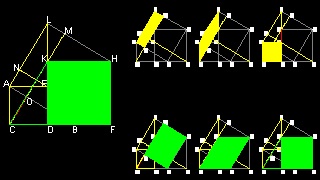
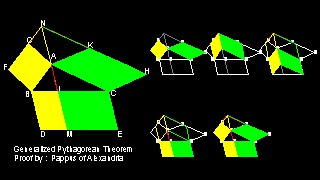
Pappus of Alexandria (およそ 290-およそ 350 AD) は 角BAC が直角でない場合には 正方形の代わりに平行四辺形を考えれば ピタゴラスの定理 と同じ様に 斜辺上の平方四辺形の面積が 他の二辺上にある平行四辺形の面積の和になることを 示した。下の図で 任意に選んだ点 H,F がその一隅となる 平行四辺形 ACHK、 ABGFを作る。 N は GF と HK の延長の交点である。 BD , CE は ともにNA に平行で その長さ は NA に等しくとる。 そのとき 次のような関係が成り立つ。 平行四辺形 BCED の面積 = 平行四辺形 ACHK の面積 + 平行四辺形 BAGF の面積
この図面とアニメーションの作成方法 :
プログラム Euclid_47.lsp をロードする。 (load "Euclid_47")
コマンド ラインから Euclid_47_4 と実行命令をタイプする。
次の証明はピタゴラスによるものと言われているが むしろ ピタゴラス学派によると言ったほうが 適切であろう。
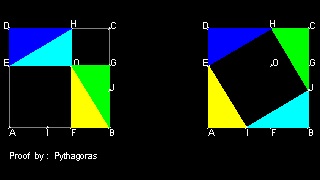
5. ピタゴラスによる証明
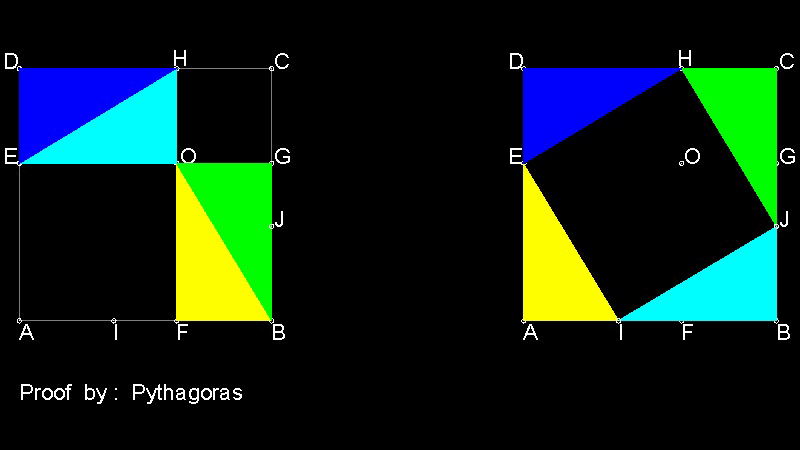
この図面とアニメーションの作成方法 :
プログラム Euclid_47.lsp をロードする。 (load "Euclid_47")
コマンド ラインから Euclid_47_7 と実行命令をタイプする。
6. 一般的 Dissection の考え方
dissection を利用した巧妙な証明がいくつかある。
dissection の 基本的な考え方を次に説明しよう。
****** tesselation_1.dwg ******
****** tesselation_2.dwg ******
****** tesselation_3.dwg ******
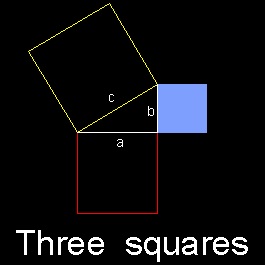
(1) 直角三角形 の三辺の長さ a,b, c を与える。 (tesselation_1.dwg)
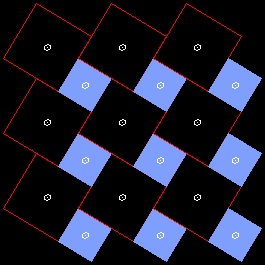
(2) 直角を挟む二辺上の正方形 (a & b) を規則的に密に並べた"AB-メッシュ" パターンを作る。 (tesselation_2.dwg)
(3) 半透明の紙に 縦、横を 等間隔(= c) にした格子線 "Cーメッシュ" を引く。 (tesselation_3.dwg)
以上の準備が出来た後、 "Cーメッシュ" を "AB-メッシュ" の上に乗せて動かす。
"Cーメッシュ" の交点 が "AB-メッシュ" の 特殊な点 (例えば 正方形の中心点とか 頂点）に来るように
して、 "Cーメッシュ" の単位正方形の領域内にある "AB-メッシュ" を切り出す。
切り出された "AB-メッシュ" は 適当に回転、平行移動することにより 元の正方形 A,B
に復元することが出来る。
"a" の 中心点の例:
この図面の作成方法 :
プログラム Euclid_47.lsp をロードする。 (load "Euclid_47")
コマンド ラインから dissection と実行命令をタイプする。
黄色の正方形で切り取った AB - メッシュ の三角形、四角形 の如何なる組み合わせでも 必ず元の二つの正方形に戻すことがで出来る。 つまりこの方法を使えば 無数の切り方が あることになる。 其の中でも興味深いのは 次の二つの場合，即ち 正方形の中心点 と 正方形の角 の場合である。
6.1 小さい正方形（ｂ）の隅を選んだ場合−１(Perigal)
この図面の作成方法 :
プログラム Euclid_47.lsp をロードする。 (load "Euclid_47")
コマンド ラインから dissection と実行命令をタイプする。
黄色の正方形の角が 小さいほうの正方形(b) の角の上に来るように動かす。
これは Perigal が 1873 年 に発表したdissection による解である。
*********** dissection_case_2.dwg ***********
Perigal による dissection(1873)
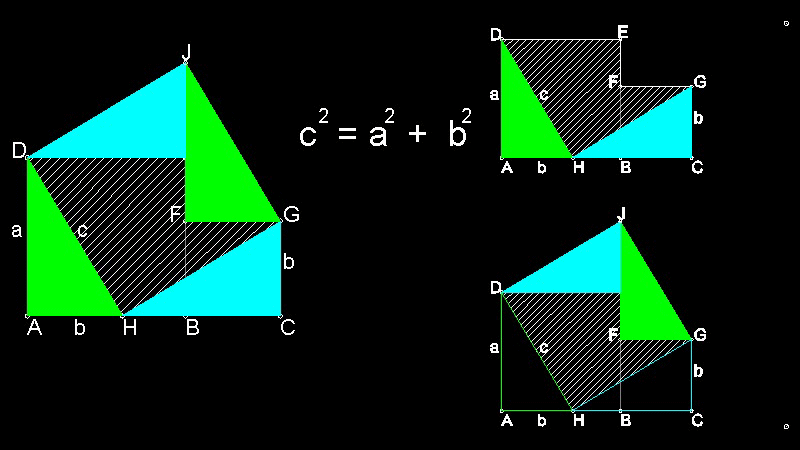
この図面とアニメーションの作成方法 :
プログラム Euclid_47.lsp をロードする。 (load "Euclid_47")
コマンド ラインから Euclid_47_2b と実行命令をタイプする。
Perigal の dissection で 斜線で示した 区域は 更に２つの３角形と一つの正方形に分割できる。 そのように すると 次のような 変形 が 考えられる。
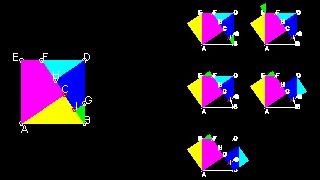
6.2 Perigal の dissection の変形
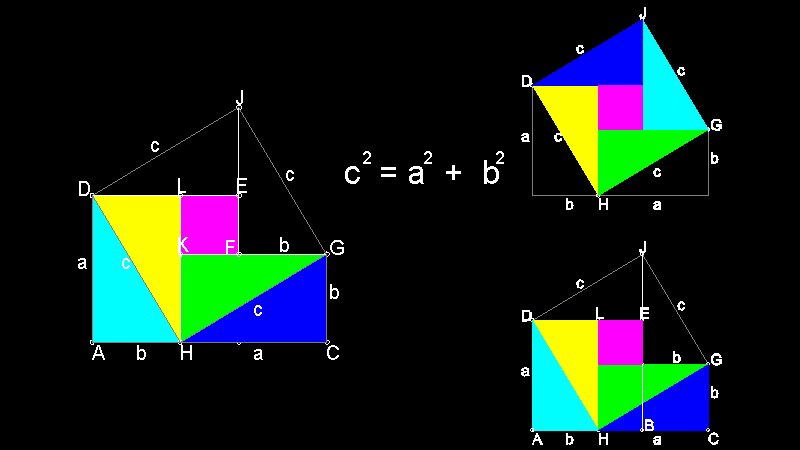
この図面とアニメーションの作成方法 :
プログラム Euclid_47.lsp をロードする。 (load "Euclid_47")
コマンド ラインから Euclid_47_2c と実行命令をタイプする。
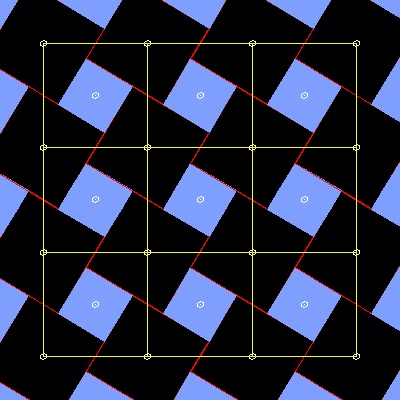
6.3 大きな正方形(a)の中心を選んだ場合 (Henry Dudeney)
この図面の作成方法 :
プログラム Euclid_47.lsp をロードする。 (load "Euclid_47")
コマンド ラインから disection と実行命令をタイプする。
黄色の正方形の角が 大きい方の正方形(a x a) の 中心に来るように動かす。
これは Henry Dudeney が 1917年 に公表したものである。
************ dissection_case_3.dwg ************
Henry Dudeney (1971) の 証明
この図面とアニメーションの作成方法 :
プログラム Euclid_47.lsp をロードする。 (load "Euclid_47")
コマンド ラインから Euclid_47_2d と実行命令をタイプする。
6.4 小さい正方形（ｂ）の隅を選んだ場合−２
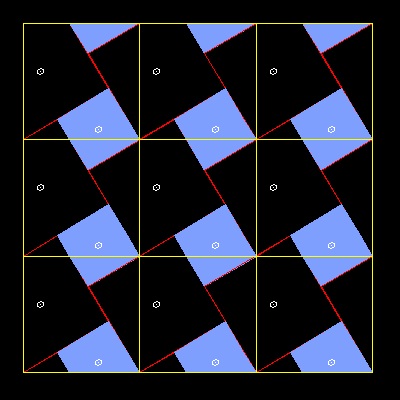
#6-1 の Perigal の解の図面の上下を逆にした後、
黄色の正方形の角 を別の (b x b) の正方形の角
に持ってくると また違った dissectionの解がみつかる。
これは 阿部 恒 の折り紙による解と同等である。
*********** origami_dissection.dwg ***********
6.5 阿部 恒 の 折り紙による証明
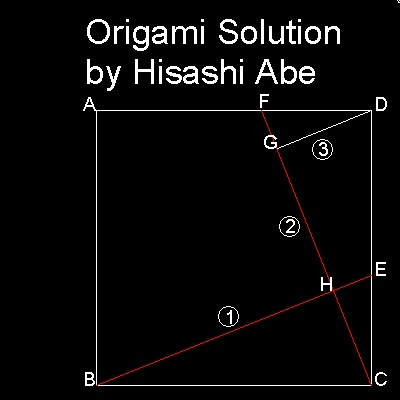
必要な物 ： 正方形の紙を一枚用意する。
折り紙の手順：
1. C を つかんで 折り目 BE をつける。 2. CD の端をつかみ点E が BE 上にくるように 折り目CF をつける。 これで CF と BE が直交している。 3. AD の端をつかみ F が CF 上にくるように 折り目GDを つける。 これで GD は CF と 直交している。 結果として、三角形BCH と CDG は合同であり、 GD = CH である ことに 注目されたい。CAD を使っての作図は簡単である。
この図面の作成方法 :
プログラム Euclid_47.lsp をロードする。 (load "Euclid_47")
コマンド ラインから Abe_origami と実行命令をタイプする。
************* Abe_origami_0.dwg *************
この準備ができたら 三角形の領域を 色鉛筆で塗り分けでおくと 見分け易くて良い。 先ず 三角形 BCH と DGC を切り抜く。 BCH を上方に動かし BC を AD に重ねる。 DGC を 左に動かし DC をAB に 重ねる。 結果の図形を見ると CH2 + BH2 = BC2 が 証明された。
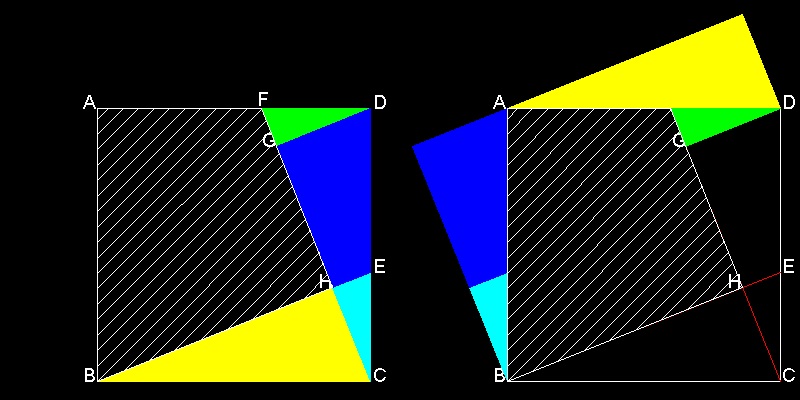
この図面とアニメーションの作成方法 :
プログラム Euclid_47.lsp をロードする。 (load "Euclid_47")
コマンド ラインから Abe_origami_a と実行命令をタイプする。
阿部 恒 の 折り紙による証明の変形
三角形 BCH と CDG は合同であるから、平行移動するかわりに BCH を Bを中心として CDG を Dを中心として 90度 回転させても 上の折り紙の結果と同じものが得られる。
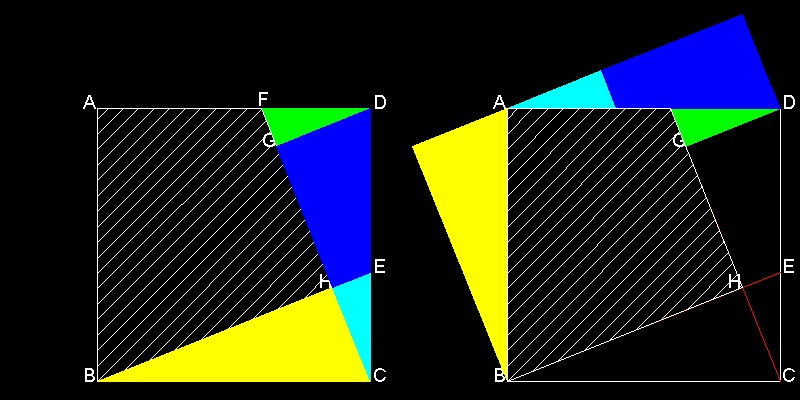
この図面とアニメーションの作成方法 :
プログラム Euclid_47.lsp をロードする。 (load "Euclid_47")
コマンド ラインから Abe_origami_b と実行命令をタイプする。
しかしこの結果は見た目が余り良くない。 その理由は ２つの小さな三角形(GDF と HCE)を 最終位置に置いたとき GFと HE の辺 に段差があり 真っ直ぐになっていないからである。 もしGH の距離を GDと同じに取れば これらの三角形は点 Fで直線としてつながる。 それを実現させたのが Mario Pacek による 次に示す証明である。
6.6 Mario Pacek の 図式解
この興味深い動画による証明は筆者が次のウェブサイト で 見かけたものである。Pythagorean Theorem by Alexander Bogomolny.
このサイトの主催者 Dr.Bogomolny によれば この証明は Mario Pacek (別名 Pakoslaw Gwizdalski) によって 公表されたものである。
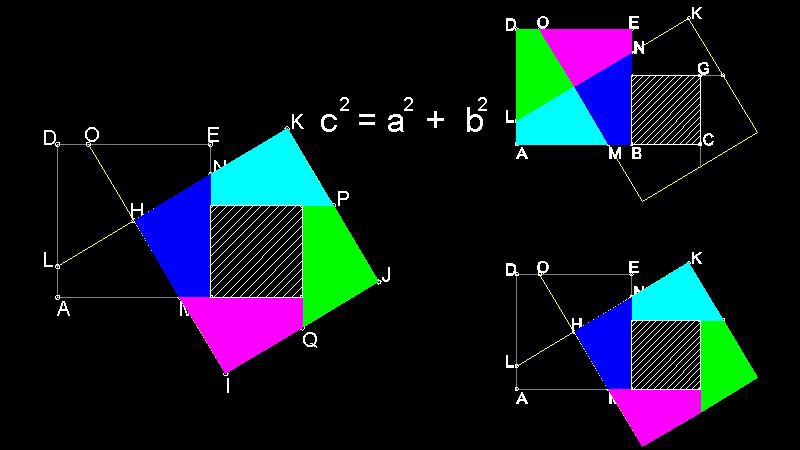
実の明快で 定理の叙述をそのまま絵にしたような素晴らしい証明である。
下の図面で HD = HI = CB になっていることに注目。
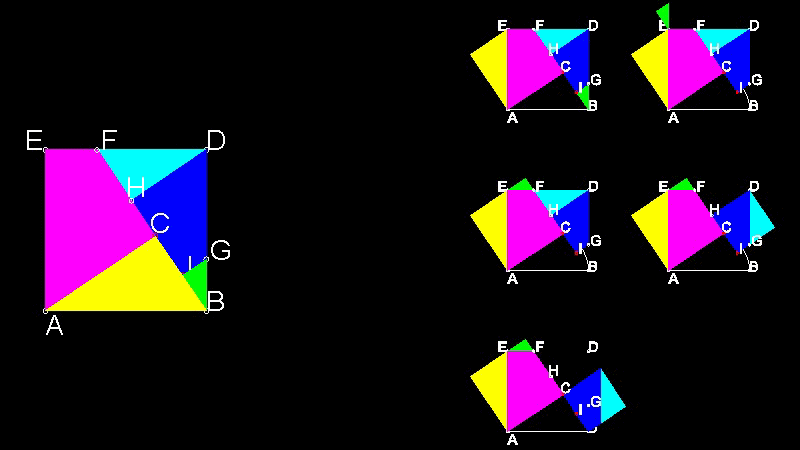********************************* Pythagorean_theorem_10.dwg *********************************
この図面とアニメーションの作成方法 :
プログラム Euclid_47.lsp をロードする。 (load "Euclid_47")
コマンド ラインから Euclid_47_8 と実行命令をタイプする。
ーーーー そのほかの巧妙な証明 ーーーー
このほかにも数多くの証明があるが その中から 特に 独創的で 際立って 美しいものだけを紹介しておく。
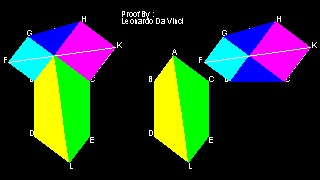
7. Leonardo Da Vinci による証明
この有名な証明は
Leonardo Da Vinci(1452-1519)
(参考 3)(p. 31)によるものである。
多方面の学問に通じていたこの天才はまた優れた数学者でもあった。
この独創的な証明は其の才能の片鱗を示している。
２つの六角形 ABDLEC と FBCKHG の面積が等しいことに注目する。 どちらの六角形も三角形ABC 2個分の面積を含んでいることから ピタゴラスの定理の証明になっている。
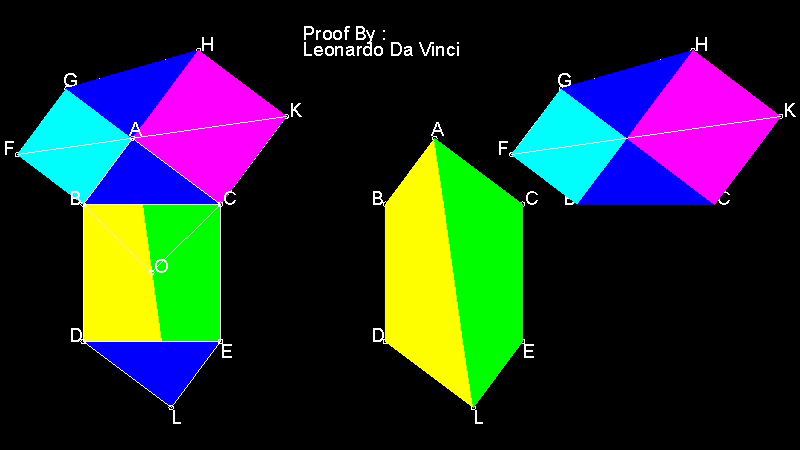
この図面とアニメーションの作成方法 :
プログラム Euclid_47.lsp をロードする。 (load "Euclid_47")
コマンド ラインから Euclid_47_5 と実行命令をタイプする。
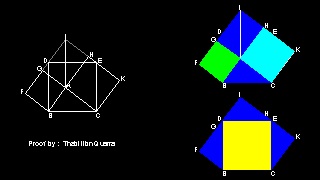
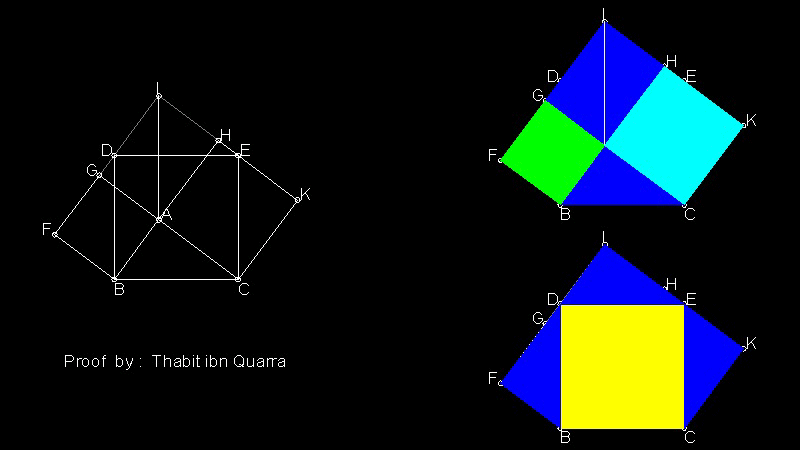
8. Thâbit ibn Quarra(828-901)による証明
この証明は Thâbit ibn Qurra(828-901)
(参考.6)(p 282-283)によるものである。
彼は トルコ に生まれ バグダッドで死んだ ９世紀のアラブを代表する偉大な数学者であった。
彼の数学上の業績についての詳細は(参考.6)を参照されたい。
五角形 FBCKI に含まれる ３個の合同な三角形を異なる箇所に 位置させることにより 直感的な 証明を導いている。
この図面とアニメーションの作成方法 :
プログラム Euclid_47.lsp をロードする。 (load "Euclid_47")
コマンド ラインから Euclid_47_6 と実行命令をタイプする。
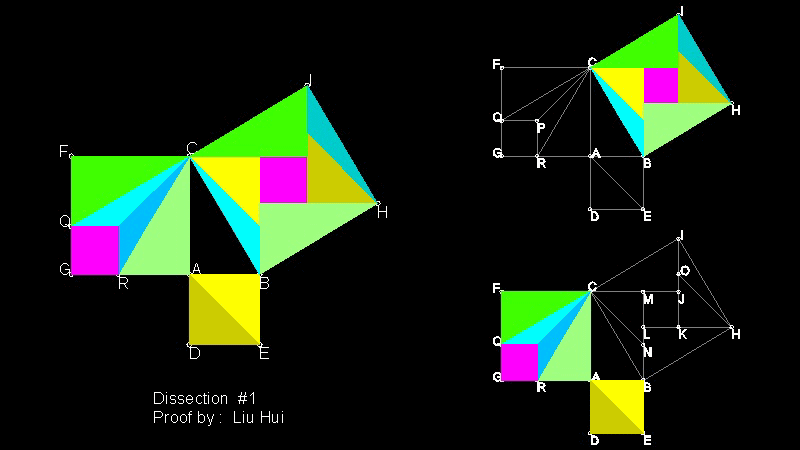
9. Liu Hui (3世紀 AD) の証明
Liu Hui(大体２２０-大体２８０) は中国の三国時代に活躍した数学者である。彼の証明は論述されたもので、 後世の研究により 再構築されたものである。
次に示す証明は其の一例である。
この図面とアニメーションの作成方法 :
プログラム Euclid_47.lsp をロードする。 (load "Euclid_47")
コマンド ラインから dissect_1 と実行命令をタイプする。
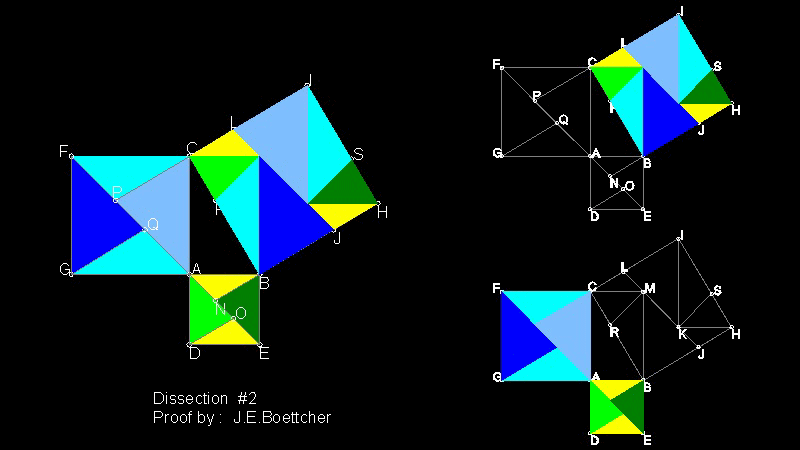
10. J.E.Böttcher による証明
参考文献 １ によると 次の証明を 幾何学的証明の １９番目に掲げ (p. 112)
Johannes Eduard Böttcher (1847 - 1919) によるものである と記している。
この図面とアニメーションの作成方法 :
プログラム Euclid_47.lsp をロードする。 (load "Euclid_47")
コマンド ラインから dissect_2 と実行命令をタイプする。
ーーーー ピタゴラスの定理の一般化 ーーーー
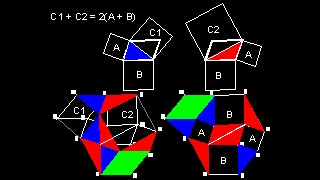
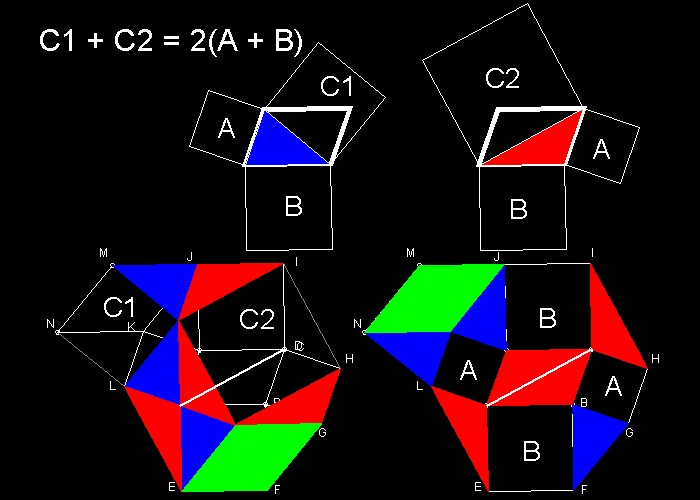
11. ピタゴラスの定理の一般化ー平行四辺形への拡張
この証明は 参考文献 ５ (p.9) から取った。
平行四辺形が 長方形の場合 (即ち C1 = C2 の時）
ピタゴラスの定理 (C = A + B ) となる。
この図面とアニメーションの作成方法 :
プログラム gen_Pythagoras.lsp をロードする。 (load "gen_Pythagoras")
コマンド ラインから gen_Pythagoras と実行命令をタイプする。
12. De Gua の定理: ピタゴラスの定理の３ 次元への拡張
De Gua の 定理はピタゴラスの定理を ３次元に拡張したもので De Gua の名の由来 は フランスの数学者
Jean Paul de Gua de Malves (1712-1785)の名前の一部である。
この定理は １７８３年にパリの科学アカデミーで発表された。
De Gua の 定理 :
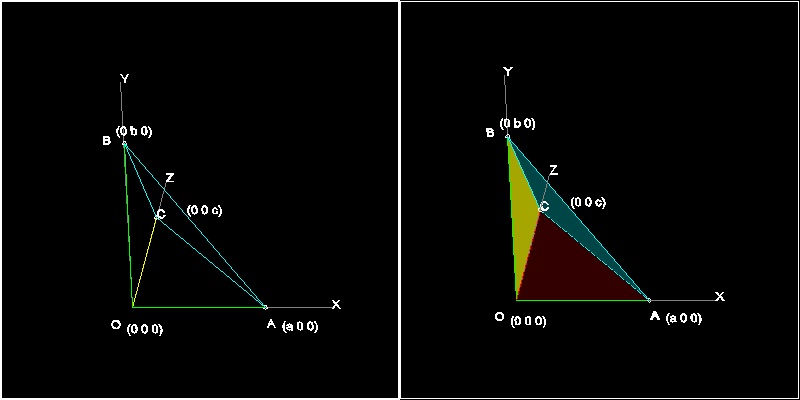
立方体を斜めに切り取った時に出来る 四面体をかんがえる。
"3 軸が直角で交わる隅に向かい合う面の面積の２乗は
他の３面の面積の２乗の和に等しい。"
つまり
(ABCの面積)2= (OABの面積)2 + (OBCの面積)2 + (OCAの面積)2
ここで OA = a, OB = b , OC = c とおけば
この定理は次のようにも表される。
(ABCの面積)2= (1/4){(ab)2 + (bc)2 + (ca)2}
この定理の証明は Heron の公式を使えば 簡単であるが 参考文献 ９ のように ピタゴラスの定理を
繰り返し使って直接 導くこともできる。
この図面の作成方法 :
プログラム DeGua.lsp をロードする。 (load "DeGua")
コマンド ラインから DeGua と実行命令をタイプする。
13. 球面座標での ピタゴラスの定理
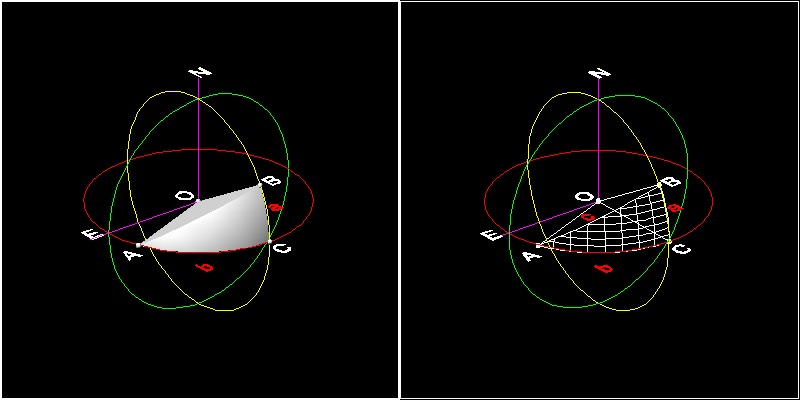
直角三角形 ABC が 半径 R の球面上にある。頂点 C が 直角で、辺の長さは a,b,c であるとき、次の様な関係が成り立つ。
cos(c/R) = cos(a/R) * cos(b/R) .
******************************* spherical_Pythagorean.dwg ********************************
この例題図の説明
赤色で示した円は 地球で言えば 赤道（緯度 ０ 度）、黄色の円は 経度 一定(例えば ０度か １８０度）の線を表している。点 A : 東経 100 度、緯度 ０度(赤道上)
点 B : 東経 180 度、北緯 ３０度
点 C : 東経 180 度、緯度 ０度(赤道上)
地球の半径は 6373 km(=3956 マイル) とした。
この図面の作成方法 :
プログラム haversine.lsp をロードする。 (load "haversine")
コマンド ラインから sphere_pythagorean と実行命令をタイプする。
SHADEMODE のコマンド を使って Gouraud shading と 3D wireframe のオプションを選ぶ。
球面座標系におけるピタゴラスの定理によると:
cos(c/R) = cos(a/R) * cos(b/R) (1)
cos(x) の Maclaurin 展開は :
cos(x) = 1 - x2/2! + x4/4! - x6/6! + ...
(1) 式に この展開を代入すると:
1 - (c/R)2/2 + (c/R)4/24 -...=
{1 - (a/R)2/2 + (a/R)4/24 -...}{1 - (b/R)2/2 + (b/R)4/24 -...}
=1 - (a/R)2/2 - (b/R)2/2 + (ab)2/(4 R4) +...
まとめると
c2 + (c の高次項)/R2
= a2 + b2 + (a と b の高次項)/R2
R の値が a,b および c, に比べ 大きい場合には、 R2 で割った項は 無視できる程小さく
その結果は 古典的な ピタゴラスの定理に落ち着く。即ち
c2 = a2 + b2
ではここにあげた例でこのことを確かめてみよう。
実例での数値の検討
上にある図面から円弧 a,b,c の長さを見つける。三次元オブジェクトにEXPLODE コマンドを使って、これ以上 EXPLODE出来ないところまで行くと
総てのオブジェクトが 線、円弧、円だけの集合になってしまう。
ここで LIST コマンドを使うと円弧の長さが得られるというわけである。
これがその結果である。
a = 3333.7534 b = 7778.7579 c = 8086.6416 and R = 6367
この結果を使って cos(a/R),等々 が計算できる。
この図面をプログラムを使って描いた場合、 其の計算は check_theorem
と言う エグゼ がやってくれて、結果は
cos(a/R) = 0.866025
cos(b/R) = 0.34202
従って cos(a/R)*cos(b/R) = 0.296198
この結果は cos(c/R) = 0.296198
と ６桁までぴったり合致している。
念のため其の比を取ると*
cos(c/R)/{cos(a/R)*cos(b/R)} = 0.99999996
となり殆ど １．０ である。
参考までに 平面でのピタゴラスの定理を使うと,
c2/{a2 + b2} = 0.91302773
となり 大きな誤差が生じることが解かる。
*注記: この計算結果は グラフィカル オブジェクトから LIST コマンドを 使って得た値を使っている。
（スクリーンに 出される 有効数字は ８ 桁までで切られている。）
三角関数、を使って a,b,c の長さを計算すれば 少なくとも １２ 桁まで正しい
結果になるはずである。
参考文献
この定理について書かれた本は多数あるが ここでは 筆者が たまたま手に入れることが出来たものだけを列挙する。
なかには すでに 廃刊になったものもあるが インターネットの古本 サイトで 見つけられることもある。
外国語版で 日本語訳の出ているものもあるとおもうが 筆者にその情報はない。
解かり次第 この部分に追加する予定である。
1. これは歴史的価値はあるが 個人の蔵書に必要とはおもえない。
2 - 6 は価値のある 参考書である。
7 は 数ある折り紙の本のなかでも 秀逸である。
ピタゴラスの定理だけに限れば 筆者は ８，９ がお勧めである。
- Loomis,Elisha Scott: The Pythagorean Proposition, NCTM, 1968. Original published in 1927.
- Wells, David: The Penguin Disctionary of Curious and Interesting GEOMETRY. London,England: Penguin Books, p.198, 1991.(Out of print)
- Eves, Howard: The Great Moments in Mathematics Before 1650,Mathematical Association of America, 1983.
- Nelson,R.B. : Proofs Without Words: Exercises in Visual Thinking. MAA, 1993.
- Nelson,R.B. : Proofs Without Words II: More Exercises in Visual Thinking. MAA, 2000.
- Swetz,F.J.: From Five Fingers to Infinity,Open Court, 1996.
- 阿部 恒: "すごいぞ 折り紙",日本評論社、2003. ISBN 4-535-78409-4
- Maor,Eli.: "The Pythagorean Theorem, A 4,000-year History",Princeton Univ.,2007.
- 大矢 真一: "ピタゴラス の 定理", 東海大学出版会, 2001.
インターネット
これまた 山ほどあるが 筆者は次の３つをお勧めします。- Pythagoras' Theorem, by Bill Casselman, The University of British Columbia.
- Many more interesting proofs by Alexander Bogomolny
- A proof of the Pythagorean Theorem by Liu Hui (third century AD)
reference for dissection Proof #9