Go to Fun_Math Content Table
Sums of Integers and Series
In finite sum of geometric series
List of animations posted on this page.(Click the text to watch animation.)
(1/4) of Triangle
(1/4) of Square
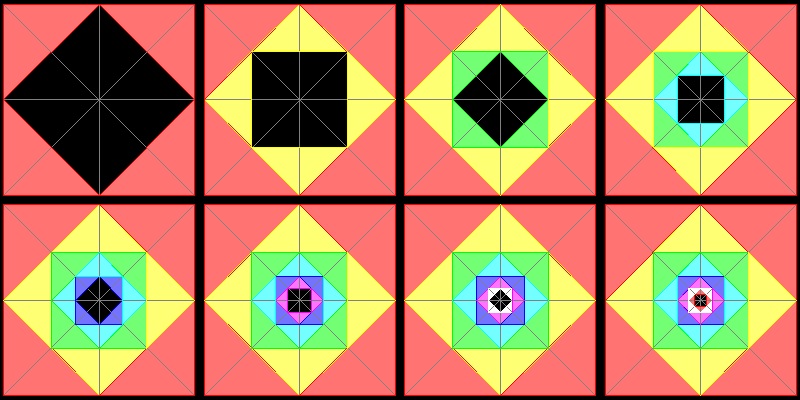
I. Basic idea - Paper Folding idea by Sundara Row (Ref. 1)
A square paper is prepared. Make 4 creases,diagonally , horizontaly and vertically as shown in the first picture.
This will define 4 middle points. Using these 4 points,fold 4 triangles as shown by red .
Area covered by red is (1/2) of the square paper.
Apply the same process to the area not colored yet. This will give the second yellow area.
The yellow colored area is (1/2) of (1/2) , which is (1/2)2.
Now the area covered by colors(red & yellow) is (1/2) + (1/2)2
and the are not covered by colors is (1/4) = (1/2)2
If this process repeated infinitely, then the colored area will eventually cover all the paper area.
This is equivalent to stating the following.
(1/2) + (1/2)2 + (1/2)3 + (1/2)4 + ... + (1/2)n+ ... = 1
We know in general (when n is not 1)that infinte sum of geometric series of (1/N)k type is 1/(n-1) .
What this example suggests is that if the process of increasing power can be done in the same pattern,
then it is possible to demonstrate a similar proof for other values of N.
********************************gss_row.dwg ********************************
Two interesting figures using triangle and square are shown in ref.2 and 3.(N = 4 case)
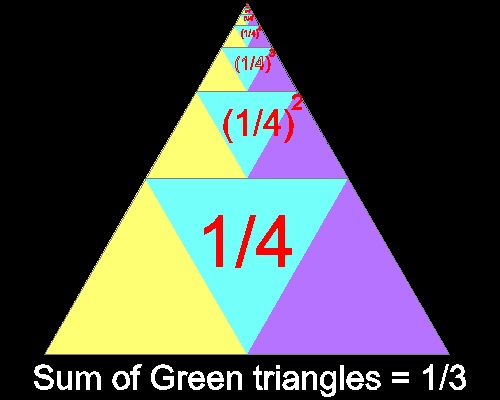
II. Triangle case
Infinite sum of geometric series with ratio = 1/4 is 1/3 as shown in the figure below.
If the area of the triangle is replaced by any arbitray angle, this same idea can be used to
do "angle trisection".
*****************gss_1_final.dwg *****************
You can see the process in animation.
To create this drawing and animation:
Load gss_1.lsp (load "gss_1")
Then from command line, type gss_1
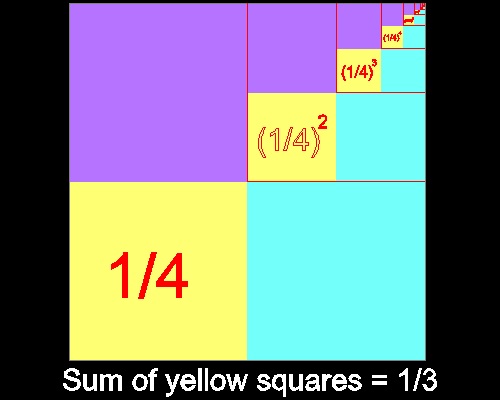
III. Square case
Infinite sum of geometric series with ratio = 1/4 is 1/3 as shown in the figure below.
*****************gss_2_final.dwg *****************
You can see the process in animation.animation
To create this drawing and animation:
Load gss_2.lsp (load "gss_2")
Then from command line, type gss_2
References
- Row, T.Sundara : Geometric Exercises in Paper Folding. Dover Publishing, p.7-8 ,1966, original in 1905.
- Nelson,R.B. : Proofs Without Words: Exercises in Visual Thinking. MAA,p.121, 1993.
- Nelson,R.B. : Proofs Without Words II: More Exercises in Visual Thinking. MAA,p.111, 2000.
Go to
Fun_Math Content Table
Sums of Integers and Series
All comments/suggestions should be sent to Takaya Iwamoto
Last Updated July 9-th, 2006
Copyright 2006 Takaya Iwamoto All rights reserved.
.


