無限幾何級数の総和(Sum of Infinite geometric series)
このページにあるアニメーションのリスト(ハイパーテキストをクリックするとアニメーションがみられます。)
ここにもどるにはブラウザーの"Back" ボタンを使う。
| 三角形の(1/4) 三角形の4分の1  |
正方形の(1/4) 正方形の4分の1 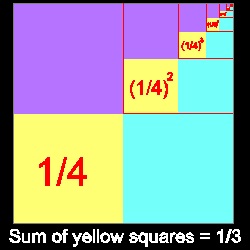 |
I. 基本的なアイデア - Paper Folding idea by Sundara Row [1]
正方形の紙を用意し、最初の図のように対角線、横、縦に4つの折り目をつける。これで4つの中間点を定義したら、赤で示した4つの三角形を折る。
赤色の領域は正方形の紙の (1/2) である。
同じ手順で色のついていない黒い部分を折る。これを二番目の黄色の領域で示す。
黄色の部分は (1/2) の (1/2) で、(1/2)2 となる。
赤と黄色の領域は (1/2) + (1/2)2 で、残りの黒い部分は (1/4) = (1/2)2 となる。
これを無限に繰り返すと、最終的に色のついた部分は紙全体となる。
これらを式で表すと、次のようになる。
(1/2) + (1/2)2 + (1/2)3 + (1/2)4 + ... + (1/2)n+ ... = 1
一般に、(n が 1 でない時)幾何級数 (1/N)k の無限和は、1/(n-1) であることが知られている。
この例は、累乗を増加する方法が同じパターンでできるならば、他のNの値についても同様に証明できることを示している。
********************************gss_row.dwg ********************************
N = 4 の場合の、三角形と正方形を使ったおもしろい図が2つ、[2 ,3]に示されている。
II. 三角形の場合
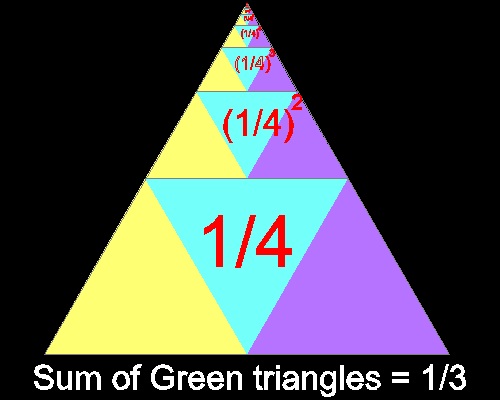
比率 = 1/4 の幾何級数の無限総和は、下図に示すように 1/3である。
このアイデアは、三角形の部分が任意の角に置き換えられるならば、"角の三等分"に適用することができる。
*****************gss_1_final.dwg *****************
この図面とアニメーションの作成方法:
プログラム gss_1.lsp を (load "gss_1") でロードする。
次にコマンド ラインから gss_1 と実行命令をタイプする。
III. 正方形の場合
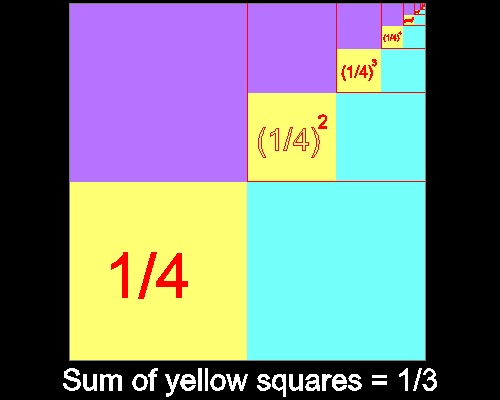
比率 = 1/4 の幾何級数の無限総和は、下図に示すように 1/3である。
*****************gss_2_final.dwg *****************
この図面とアニメーションの作成方法:
プログラム gss_2.lsp を (load "gss_2") でロードする。
次にコマンド ラインから gss_2 と実行命令をタイプする。
参考文献
- Row, T.Sundara : Geometric Exercises in Paper Folding. Dover Publishing, p.7-8 ,1966, original in 1905.
- Nelson,R.B. : Proofs Without Words: Exercises in Visual Thinking. MAA,p.121, 1993.
- Nelson,R.B. : Proofs Without Words II: More Exercises in Visual Thinking. MAA,p.111, 2000.
ホームページの内容目次に戻る 整数の総和、級数の総和
質問、問い合わせは 筆者 岩本 卓也 宛てにお願いします。
Last Updated July 9-th, 2006
Copyright 2006 Takaya Iwamoto All rights reserved. .