三乗総和

 ホームページの内容目次に戻る  整数の総和、級数の総和

整数の三乗総和 (Sum of integers cubed)

このページにあるアニメーションのリスト（ハイパーテキストをクリックするとアニメーションがみられます。）
ここにもどるにはブラウザーの"Back" ボタンを使う。

三乗総和 - 1
対角線に正方形を置く方法
i		 三乗総和 - 2
階段状ピラミッドを回転させる方法
i

フィボナッチ(Fibonacci)によるエレガントな証明

[2, 4]
下の図式に示すように、１から始まる奇数の総和は、その二乗で与えられる。 

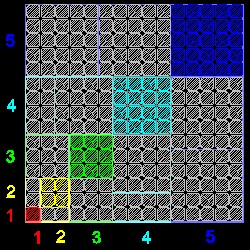
                 1                              =  12
             1 + 3                            =  22
           1 + 3 + 5                          =  32
         1 + 3 + 5 + 7                        =  42
       1 + 3 + 5 + 7 + 9                      =  52
     1 + 3 + 5 + 7 + 9 + 11                   =  62

このパターンの一解釈法は、"N行目の平均値はNである！！"
そこで、行の和、即ち奇数の和は NxN=N2 となる。
これは、前の整数のところで説明したことである。

フィボナッチ(Fibonacci, 1170-1250) は、同じ奇数を次のように違ったパターンで配置し、
整数の三乗総和に関するエレガントな証明をした。 

                  1                             =  13
              3 + 5                           =  23
            7 + 9 + 11                        =  33
        13 + 15 + 17 + 19                     =  43
      21 + 23 + 25 + 27 + 29                  =  53
   31 + 33 + 35 + 37 + 39 + 41                =  63
フィボナッチ(Fibonacci)によるこの表の解釈は上と同じ。
"N行目の平均値はN2である！！"
それで、N行目はN項を持ち、その平均値は N2 となる。
従って、行の総和は N2 x N = N3 である。

ここで左側を見てみる。
N行目の奇数の最後の項が、三角数TNであるのは、
TN = 1 + 2 + .. + N　からである。
よって、最初の p 奇数の総和は p2 であることが判る。
このことから、フィボナッチ(Fibonacci)は次の式を導いた。
      13+ 23+ 33+ ... + N3 = (1 + 2 + 3 + ... + N)2 = (TN)2 = {(1/2)N(N+1)}2

方法 2

[1, 3]
フィボナッチの図式と下図を比較する。フィボナッチの図式での平均値は、対角線位置の正方形で表される。
N=6 の場合　を例でしめす。
ここをクリックしてアニメーションを見る。

左図から次のことがわかる。
小さな正方形の総数　は　  13 + 23 + 33 + 43 + .. + N3
全体の正方形の一辺の長さは　  1 + 2 + 3 + 4 + ... + N
したがって次の関係が成り立っていることがわかる。
  13 + 23 + 33 + 43 + .. + N3 = (1 + 2 + 3 + 4 + .. + N)2

三角数("Triangular Number")の定義を思い出して
  Tn = 1 + 2 + 3 + ... + n = (1/2)N(N+1)
よって、
    13 + 23 + 33 + 43 + .. + N3 = (1/4){N(N+1)}2


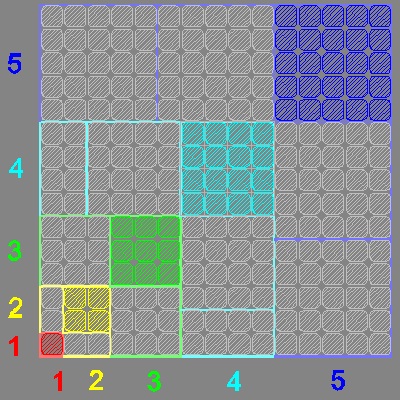
この図面とアニメーションの作成方法：
  プログラム sumcube_2.lsp　を　(load "sumcube_2")　でロードする。
  次にコマンド ラインから　sumcube_2　と実行命令をタイプする。


******************sumcube_2.dwg ******************

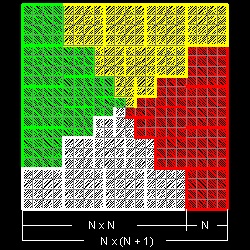
ここで、下の左図に示すように、タイルのパターンの左上の部分を切り離す。
これを時計回りに90度回転し、（1,2,3,4,5の番号の付いた）横線に重なるようにすると、右側に示すような階段状のパターンができる。
この階段を元の正方形の中心の赤タイルの周りに90度づつ４回、回転すると正方形になることがわかる。
これを利用すると次のビジュアル化が可能になる。

















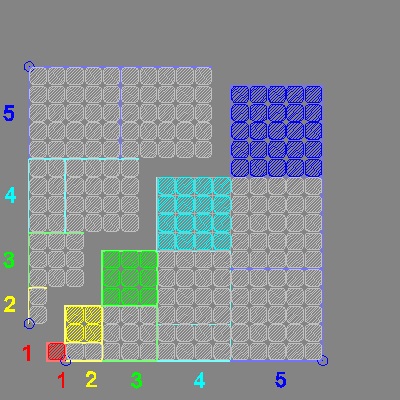
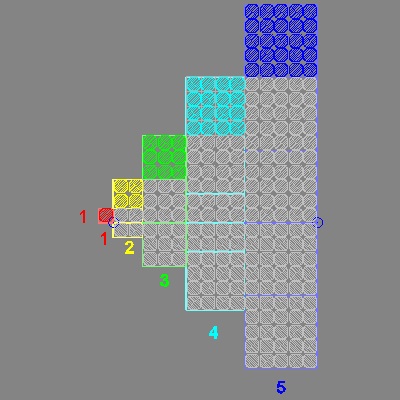
******************sumcube_2_1.dwg *****************  ****************sumcube_2_2.dwg ******************

方法 3

[3]　上述のごとく　上右図　のパターンを、円周方向に4回コピーすると正方形を形成する。
そのとき　正方形の一辺の長さは　上右図で （1+2+3+4+5) の２倍　、つまり　2 Tn　であるから,
1 ～ N の三乗総和が次のように求まる。
    Sn = 1 + 23 + 33 + 43 + ... + N3   とおくと
    4 x Sn = {N (N + 1)}2
よって、   Sn = (1/4){N (N + 1)}2
N=4 の場合を例として示す。
ここをクリックしてアニメーションを見る。


**********************sumcube_1_final.dwg **********************

この図面とアニメーションの作成方法：
  プログラム　sumcube_1.lsp　を　(load "sumcube_1")　でロードする。
  次にコマンド ラインから　sumcube_1　と実行命令をタイプする。

参考文献

  1. Wells, David: The Penguin Dictionary of Curious and Interesting GEOMETRY. London,England: Penguin Books, p.198, 1991.(Out of print)

  2. Conway,J.H., Guy,R.K.: The Book of Numbers. Springer-Verlag,New York, p 27, 1995.

  3. Nelson,R.B. : Proofs Without Words: Exercises in Visual Thinking. MAA,p.85,87, 1993.

  4. Dantzig, Tobias : NUMBER, The Language of Science. New York: The Free Press, p.269, 1930.
  ホームページの内容目次に戻る  整数の総和、級数の総和

質問、問い合わせは　筆者 岩本　卓也　宛てにお願いします。

Last Updated July 9-th, 2006

Copyright 2006 Takaya Iwamoto   All rights reserved. .