等間隔に並べられた Ｎ個の数の総和（等差数列）
(Sum of N equally spaced numbers)
このページにあるアニメーションのリスト（ハイパーテキストをクリックするとアニメーションがみられます。）
ここにもどるにはブラウザーの"Back" ボタンを使う。
| 三角数 連続する三角数が正方形になる  |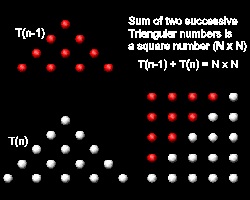
整数の和 (1) 自然数の和 －その １  |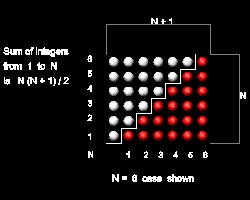
整数の和 (2) 自然数の和 －その ２  |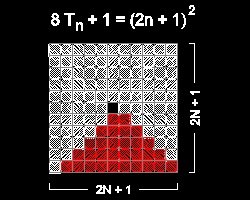
| 奇数の和 そのー１ 奇数の和 が正方形を作る  |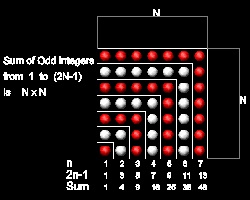
奇数の和 そのー2 奇数の和 ４個が正方形を作る  |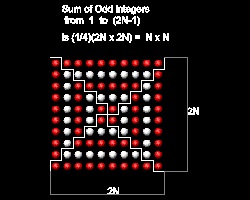
等差数列の一般例 一般の等差数列の総和  |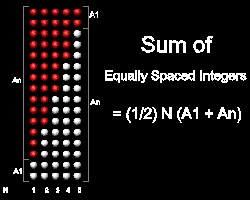
1. 自然数の総和 (I)
自然数の級数で、連続する項の和が三角数であるということを発見したのは、
おそらくピタゴラス
Pythagoras of Samos, (およそ 569-475 BC)
である。[3]
ピタゴラスはピタゴラス学派と呼ばれる一種のカルト集団の精神的主導者 で そこで発見された数学的業績は個人でなく
団体のものとされたので、
ピタゴラス と名の付いた数々の業績のうち ピタゴラス 個人がどのくらい貢献したのかは明白でない。
************************* triangular_number.dwg *************************
ギリシャの数学者達は、二つの連続する三角数が正方形の形状を形成する、ということは判っていた。
1からNまで自然数を並べた 三角数の総和 を Tnと呼ぶことにすると
Tn = 1 + 2 + 3 + ... + N
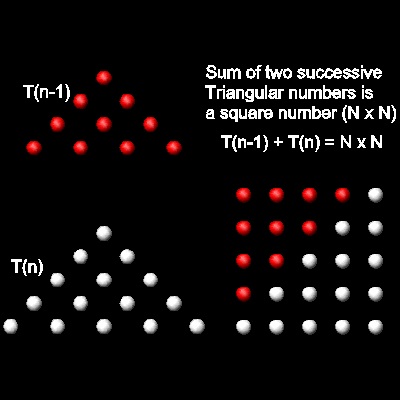
ここをクリックしてアニメーションを見る。
左の図から次の関係が成り立つことがわかる。
Tn-1 + Tn = N2
N を両サイドに加えると、
(Tn-1 + N ) + Tn = 2Tn = N2 + N = N(N + 1)
これから よく知られた 1 から N までの自然数の総和の式
Tn = (1/2)N(N + 1)
が得られる。
この図面とアニメーションの作成方法：
プログラム sumtrig.lsp を (load "sumtrig") でロードする。
次にコマンド ラインから sumtrig と実行命令をタイプする。
注*： このプログラムは white_ball.dwg と red_ball.dwg が必要です。
*************** sumtrig_final.dwg ******************
この結果は次のデモにつながります。
自然数の総和 1 ～ N = (1/2) N (N + 1) [2](p.69)
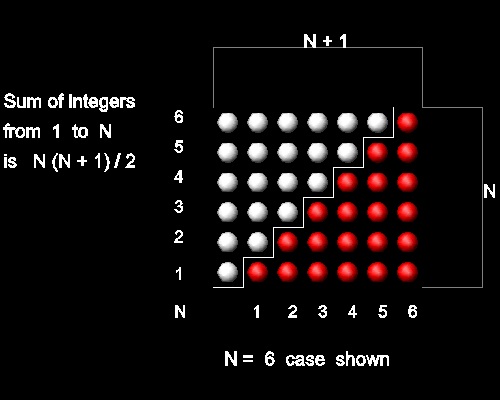この図では、１～Ｎの和の二倍が N(N+1) であること、
または 2 Tn = N (N + 1) であることを表している。
よって Tn = (1/2) N (N + 1) となる。
N = 6 の場合 ここをクリックしてアニメーションを見る。
この図面とアニメーションの作成方法：
プログラム sumint_1.lsp を (load "sumint_1") でロードする。
次にコマンド ラインから sumint_1 と実行命令をタイプする。
注*： このプログラムは white_ball.dwg と red_ball.dwg が必要です。
*********************sumint_1_final.dwg *********************
2. 自然数の総和 (II)
もう一つの方法では、三角数を階段"staircase"方式で並べ替えて、矩形数("oblong" number)の項を考える。
[3] によれば、最初にピタゴラス学派が発見したのは、矩形数が三角数の倍であるということであった。
ここでは矩形数を n(n+1) で表す。
ギリシャの数学者達は、矩形数と正方形には関係があり、
それが 4 'oblong' + 1 で正方形を作るということは判っていた。
左の図は、そのことを示している。
一矩形数は、二個の等しい三角数によって作られるので、
この図では、"８つの三角数 + 1 = 矩形数" であることを表している。
白いタイルブロックとを合わせると、ピラミッドのようなブロックが
中心の正方形の周りに形成される。 よって、４つの矩形ブロックの代わりに、この新しいブロックを
４つ組み合わせた正方形全体を見ることができる。
このアイデアは次のビジュアル化につながる。[5]
****************sumint_2_oblong.dwg ****************
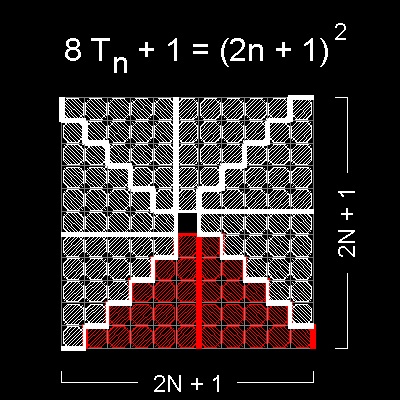"８つの三角数 + 1 =
矩形数" は次の式で表される。
8 Tn + 1 = (2n + 1)2
従って 8 Tn = (2n + 1)2 - 1 = 4 n(n+1)
そしてよく知られている Tn = n(n+1)/2
ここをクリックしてアニメーションを見る。
この図面とアニメーションの作成方法：
プログラム sumint_2.lsp を (load "sumint_2") でロードする。
次にコマンド ラインから sumint_2 と実行命令をタイプする。
注*： このプログラムは white_hatch.dwg が必要です。
************sumint_2_final.dwg ************
3. 自然数の奇数の総和 (I)
下図に示すように、自然数の奇数 1 ～ 2N-1 の総和は N2 で表される。
これは正方形を作るので、この総和は二乗数"square" numberと呼ばれている。[3, 4]
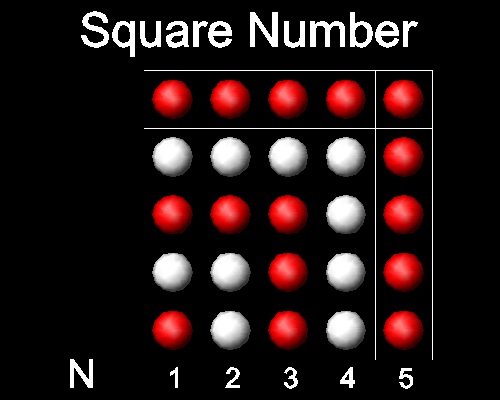
***************** square_number.dwg *****************
[3]からの引用 : "多数のドット（例えば図に示すように16個のドット）があり、それで正方形を作るとすると、
次の大きな正方形。つまり５の正方形は、図のようにドットの行を前の正方形の二辺に並べていくことで作ることができる。
加えた数は 2.4 + 1 = 9 である。この連続した正方形を作る方法は、最初の正方形の数１からはじめてずっと適用できる。
１に加える連続な数は、上の図に示すように 3, 5, 7, .....(2n+1)で、いわゆる連続した奇数である。
この方法は、１から始まる連続な奇数 1,3,5,7 ....の級数項の和が正方形となることを示す。
実際に、1 + 3 + 5 + ....+ (2n - 1) = n2 である。一方、次の奇数が (2n + 1) の場合は、次の大きな正方形が、 (n+1)2
となる。 これらは全てピタゴラスには判っていた。"
注記： N2 + 2N + 1 = (N + 1)2
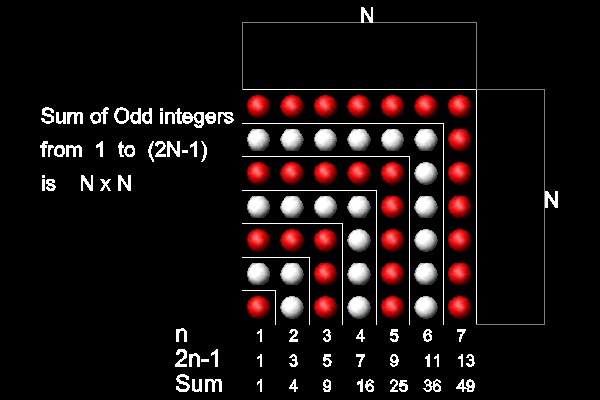
N = 7 の場合 ここをクリックしてアニメーションを見る。
この図面とアニメーションの作成方法：
プログラム sumodd_1.lsp を (load "sumodd_1") でロードする。
次にコマンド ラインから sumodd_1 と実行命令をタイプする。
このプログラムは red_ball.dwg と white_ball.dwg が必要です。
************************sumodd_1_final.dwg ************************
下図に示すように、上の対角線部分を左へ移動し、時計回りに90度回転させ、右の三角形を作る。
左から右へ、その順番は1, 3, 5, ... ,の奇数である。
このアイデアは次のビジュアル化につながる。
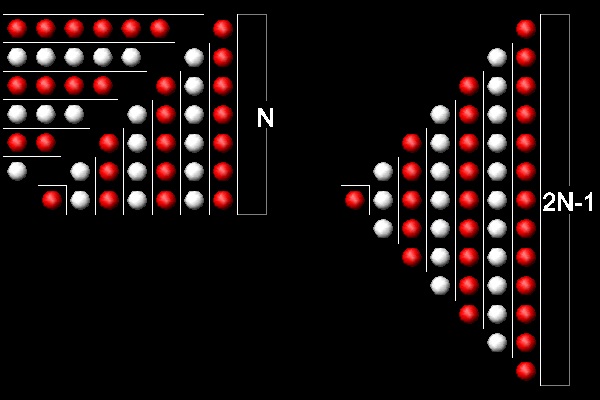
************************sumodd_1_a.dwg ************************
4. 自然数の奇数の総和 (II)
下図に示すように、奇数 1 ～ 2N-1 の和は N2 と表される。[2](p.72)
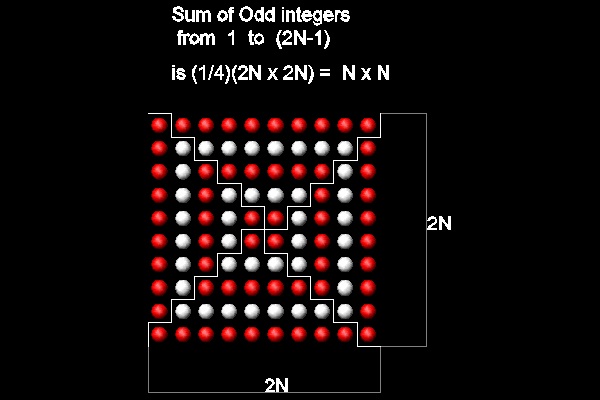
N = 5 の場合 ここをクリックしてアニメーションを見る。
この図面とアニメーションの作成方法：
プログラム sumodd_2.lsp を (load "sumodd_2") でロードする。
次にコマンド ラインから sumodd_2 と実行命令をタイプする。
このプログラムは red_ball.dwg と white_ball.dwg が必要です。
************************sumodd_2_final.dwg ************************
5. 一般化：等配分された数Ｎの総和
[1] 上記に述べた等差数列は、等間隔にならんだ数 Ｎの和の特別なケースとして取り扱うことができる。
等間隔にならんだ数 Ｎの等差数列は、次のように定義される：
An = A1 + N x d, （d は定数、N=1,2,3,....）
A1 =
1 の時 d=1 は自然数、d=2 奇数。
一般に A1 と d は実数で、整数である必要はない。
そこで、最初のN項の総和は Sn =
(1/2)N(A1 + An) となる。
例：
総和 1,2, 3, ..., N = (1/2)N(A1 + An) = (1/2)N(1 + N)
総和 1,3,5,..(2N-1) = (1/2)N(A1 + An) = (1/2)N{1 + (2N-1)} = (1/2)N*2N = N2
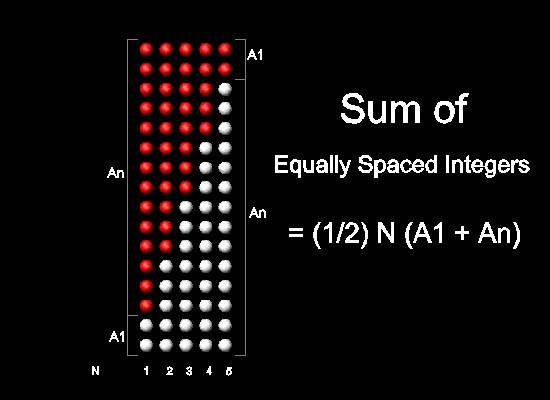A1=2, d = 3, N = 5 の場合 ここをクリックしてアニメーションを見る。
この図面とアニメーションの作成方法：
プログラム sumint_3.lsp を (load "sumint_3") でロードする。
次にコマンド ラインから sumint_3 と実行命令をタイプする。
このプログラムは red_ball.dwg と white_ball.dwg が必要です。
*************arithmetic_progression_final.dwg *************
参考文献
- Conway,J.H., Guy,R.K.: The Book of Numbers. Springer-Verlag,New York, p.33, 1995.
- Nelson,R.B. : Proofs Without Words: Exercises in Visual Thinking. MAA, p.69, 1993.
- Heath, Sir L.H.: A manual of Greek Mathematics. Dover Edition ,p.43, 1963. Originally published in 1931.
- Wells, David: The Penguin Dictionary of Curious and Interesting NUMBERS. London,England: Penguin Books, p.85, 1986.
- Wells, David: The Penguin Dictionary of Curious and Interesting GEOMETRY. London,England: Penguin Books, p.198, 1991.
- Dantzig,Tobias: NUMBER, The Language of Science. New York: The Free Press, p.41-43, 1930.