整数の二乗総和
このページにあるアニメーションのリスト(ハイパーテキストをクリックするとアニメーションがみられます。)
ここにもどるにはブラウザーの"Back" ボタンを使う。
| 三角錐数と三角数の関係 三角数から三角錐数を求める 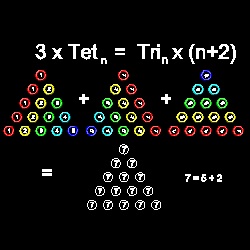 |
二乗総和 vs. 三角数 三角数から二乗総和を求める 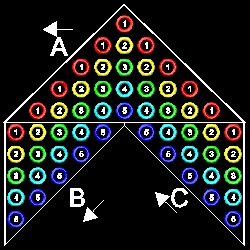 |
二乗総和に関する3Dアニメーション 三次元アニメーション  |
三角錐数と四角錐数
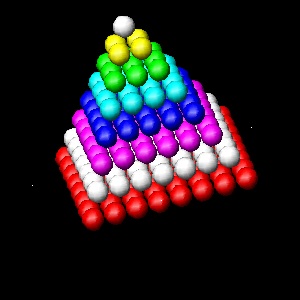
整数 1 ~ N の二乗総和は、球の各層が正方形の形状を形成することから、四角錐数("Square Pyramid Numbers")
とも呼ばれ,次のように表わされる。(下の左図)
Pyrn = 12 + 22 + 32 + ... + N2
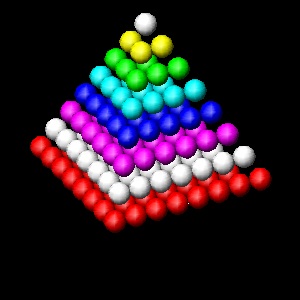
***********square_pyramid.dwg *********
*********tetrahedral_pyramid.dwg *******
第一層:1 = T1 = 1
第二層:1 + (1 + 2) = T1 + T2 = 4
第三層:1 + (1 + 2) + (1 + 2 + 3) = T1 + T2 + T3 = 10
第四層:1 + (1 + 2) + (1 + 2 + 3) + (1 + 2 + 3 + 4) = T1 + T2 + T3 + T4 = 20
等。
これは、三角数 Tnの和であり、三角錐数(tetrahedral number)と呼ばれる。
即ち Tetn = T1 + T2 + T3 + .... + Tn
連続する二つの三角数が二乗数を作ることはすでに述べた。これに類似した法則は、四角錐にも存在する。 即ち、
四角錐数は連続した二つの三角錐数から作ることができる。
四角錐数と三角錐数の関係は、次の二つの図を見ても容易に理解できる。
下図は、四角錐数が二つの三角錐数らか作られることを示している。この例では、
Pyr5 = Tet4 + Tet5 で、一般式は
Pyrn = Tetn-1 + Tetn
と表される。
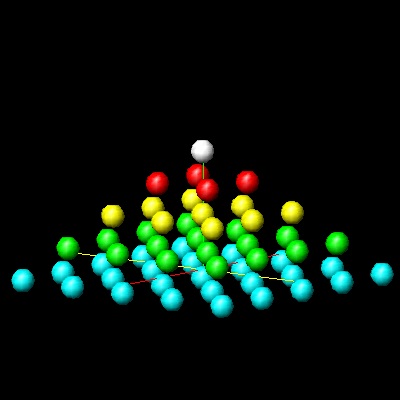
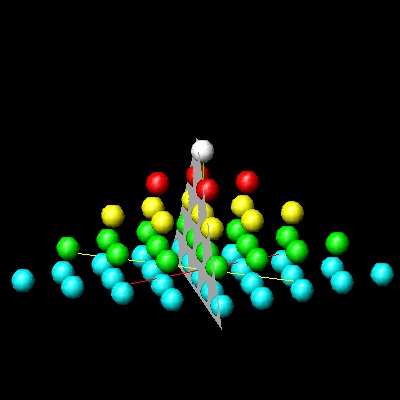
**************square_pyramid_final.dwg ************* ***************square_pyramid_cut.dwg **************
この図面の作成方法:To create this drawing :
プログラム sumsqr_1.lsp を (load "sumsqr_1") でロードする。
次にコマンド ラインから square_pyramid と実行命令をタイプする。
スペース間隔には 2.0~2.5 を指定する。1.5 の時にきっちりと詰まる。
次のコマンドで中央の平面を描く: cut_plate
注*: このプログラムは
red_ball.dwg ,yellow_ball.dwg ,green_ball.dwg ,cyan_ball.dwg
blue_ball.dwg ,magenta_ball.dwg ,white_ball.dwg が必要です。
[1](p.45) では、三角錐数を使うと n 番目の三角錐数( Tetn )の式が
Tetn = (1/6) n(n+1)(n+2)
となる、という非常におもしろいビジュアルな証明をしている。
下図では 理解を助けるために それぞれの数字を異なる色のリングで表わした。
数字の 1,2,3,4,5 に それぞれ 赤、黄、緑、シアン、青 の色を対応させた。
この説明は N = 5 の場合についてである。
ここをクリックしてアニメーションを見る。
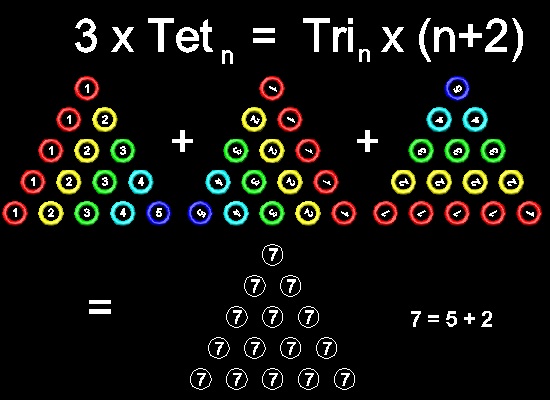
この図面とアニメーションの作成方法:
プログラム sumsqr_3.lsp を (load "sumsqr_3") でロードする。
次にコマンド ラインから sumsqr_3 と実行命令をタイプする。
注* : このプログラムは
red_1_ring.dwg ,yellow_2_ring.dwg
green_3_ring.dwg ,cyan_4_ring.dwg
blue_5_ring.dwg ,magenta_6_ring.dwg
white_7_ring.dwg が必要です。
*********************sumsqr_3_final.dwg *********************
この図で、上の段の三角形は いずれも 5 までの三角数(Tetrahedral number) Tet5
つまり 三角数 T1 から T5までの 総和、すなわち
Tet5 = T1+ T2 + T3+T4 + T5
を表わしている。
上方の行 --一番目の三角形: Tet5
上方の行 --二番目の三角形: 一番上の先端を回転軸にして一番目の三角形を時計回りに120度回転する。
上方の行 --三番目の三角形: 一番上の先端を回転軸にして二番目の三角形を時計回りに120度回転する。
下方の行: 同じ位置における円内の全ての数を加算する。すると、円の総数は5番目の三角錐数が
(T5 = 1 + 2 + 3 + 4 + 5 ) であることに注目。
そこで、この図が 3 x Tet5 = T5 x (5 + 2) であることを示す。
一般的には 3 x Tetn = Tn x (n + 2) = (1/2)n (n + 1) (n + 2) で表される。
故に、
Tetn = (1/6) n(n+1)(n+2) である。
四角錐数 と 三角錐数 の関係:
Pyrn = Tetn-1 + Tetn を使うと
四角錐数は、次のように表される。
Pyrn = Tetn-1 + Tetn = (1/6)(n-1)n(n+1) + (1/6)n(n+1)(n+2) = (1/6)n(n+1)(2n+1)
1. 二乗総和 (二次元的な説明-Planar Approach)
[1] では、前の部分で述べた次の二つの結果を用いて二次元的な説明をしている。1. 連続した三角数を加算すると正方形を成す、または Tn-1 + Tn = n2 となる。
2. 三角数: Tn = (1/2)n(n+1)
この図面とアニメーションの作成方法:
プログラム sumsqr_2.lsp を (load "sumsqr_2") でロードする。
次にコマンド ラインから sumsqr_2 と実行命令をタイプする。
************sumsqr_2_final.dwg ***********
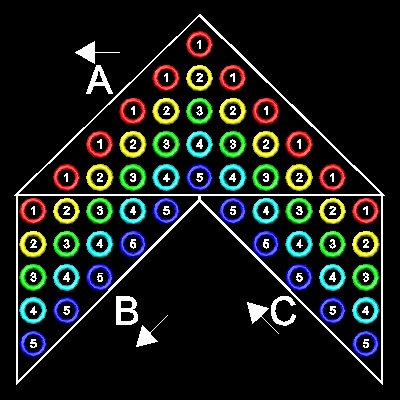
N=5 の場合の例を示す。中心線に、T5の列を描く。 そして、両サイドに Tn の N (= 5) 個のコピーを作る。 列の総数は (2N + 1) (= 11) である。 次に、3つのグループ A, B, C を作る。 3つのグループ数の総和を、図の矢印方向に行う。 グループ A: 上からスタートすると、1 , 1+2+1, 1+2+3+2+1, 1+2+3+4+3+2+1,... である。 各項が連続した二つの三角数の和であるから、項はそれぞれ二乗の数になる。 よってこれらの総和は、 Sn=1+22+32+42+52 グループ B: 赤の列: 1x1 黄の列: 2 x 2=22 緑の列: 3 x 3=32 シアンの列: 4 x 4=42 青の列: 5 x 5=52 これらを加えると 1+22+32+42+52 、そこで、これは二乗数の総和 (Sn) である。 グループ C: B と同じで、総和は Sn である。 このように、(2N+1)個の三角数 Tn のコピーと3つのグループの二乗総和が得られる。 よって 3 Sn = (2N+1)Tn = (2N +1)N(N+1)/2 すなわち Sn = (2N +1)N(N+1)/6
2. 二乗総和 (3次元アプローチ)
ビジュアルな見地からすれば、[2]で示されているものが一番直感的である。次の図は、N=5 の場合の最初と最後のステップを示している。
詳細は ここをクリックしてアニメーションを見る。
******* x, y, z軸に並行に並べた3個の等しいブロックは、一個のブロックに組み立てられる。*******

 ***************sumsqr_1_start.dwg **************
***************sumsqr_1_final.dwg **************
***************sumsqr_1_start.dwg **************
***************sumsqr_1_final.dwg **************
最後のブロックの容積は、上に示されるように N(N+1){N+(1/2)} である。
これは、3つのブロックから作られるため、各々の二乗の和は、 1 + 22+ 32+ ...+ N2,
3 (1 + 22+ 32+ ...+ N2) = 3 Sn = N(N+1){N+(1/2)} , または
Sn = (1/6)N(N+1)(2N+1) によって表される。
この図面とアニメーションの作成方法:
プログラム sumsqr_1.lsp を (load "sumsqr_1") でロードする。
次にコマンド ラインから sumsqr_1 と実行命令をタイプする。
筆者の注記:このプログラムは、理由は判らないが、3ブロックをまとめると停止してしまう。
プロセスを継続する際には、次のコマンドを実行する
explode
!ss3
その後 "リターン" キー を押す。そして
finish_up
とタイプする。
注*: このプログラムは
red_cube.dwg ,yellow_cube.dwg ,green_cube.dwg ,cyan_cube.dwg
blue_cube.dwg ,magenta_cube.dwg ,white_cube.dwg が必要です。
参考文献
- Conway,J.H., Guy,R.K.: The Book of Numbers. Springer-Verlag,New York, p 27, 1995.
- Nelson,R.B. : Proofs Without Words: Exercises in Visual Thinking. MAA, p.77, 1993.
ホームページの内容目次に戻る 整数の総和、級数の総和
質問、問い合わせは 筆者 岩本 卓也 宛てにお願いします。
Last Updated Sept 9-th, 2006
Copyright 2006 Takaya Iwamoto All rights reserved. .