Sum of integers cubed

Go to   Fun_Math Content Table   Sums of Integers and Series

Sum of integers cubed

List of animations posted on this page.(Click the text to watch animation.)
Sum of cube - 1
Sum of cube - 2

Fibonacci's elegant proof

(Ref. 2, 4)
Sum of odd integers,starting with 1, gives the square as shown in the diagram below. 
               1                              =  12
             1 + 3                            =  22
           1 + 3 + 5                          =  32
         1 + 3 + 5 + 7                        =  42
       1 + 3 + 5 + 7 + 9                      =  52
     1 + 3 + 5 + 7 + 9 + 11                   =  62
One way to interpret this pattern is "the average number of the N-th row is N !!"
Therefore the sum of the row,which is the sum of odd integers, is NxN=N2.
This is what we has been discussed in the previous section on integer.

Fibonacci(1170-1250) arranged the same odd numbers in a different pattern as shown below
and came up with a very elegant proof regarding the sum of integers cubed. 

                1                             =  13
              3 + 5                           =  23
            7 + 9 + 11                        =  33
        13 + 15 + 17 + 19                     =  43
      21 + 23 + 25 + 27 + 29                  =  53
   31 + 33 + 35 + 37 + 39 + 41                =  63
Fibonacci's interpretation of this table is the same as above.
"the average number of the N-th row is N2 !!"
So the N-th row has N terms and their average is N2.
Therefore the sum of the row is N2 x N = N3.

Now let us take a look at the left hand side.
The last term of the odd integer on the N-th row is a triangular number TN,
because TN = 1 + 2 + .. + N
And we know that sum of the first p odd integers is p2
Therefore Fibonacci concluded
      13+ 23+ 33+ ... + N3 = (1 + 2 + 3 + ... + N)2 = (TN)2 = {(1/2)N(N+1)}2

Method 2

(Ref. 1 ,3)
Compare the figure below with Fibonacci's diagram. The average numbers in Fibonacci's diagram
are now represented by squares in the diagonal position.

You can see the process in animation for N=6 case.
It is easy to figure out the following relation.
  13 + 23 + 33 + 43 + .. + N3 = (1 + 2 + 3 + 4 + .. + N)2

Please recall the "Triangular Number"
  Tn = 1 + 2 + 3 + ... + n = (1/2)N(N+1)
So Sum of cube from 1 to N = (1/4){N(N+1)}2


To create this drawing and animation:
  Load sumcube_2.lsp ---> (load "sumcube_2")
  Then from command line, type sumcube_2

**************sumcube_2.dwg **************

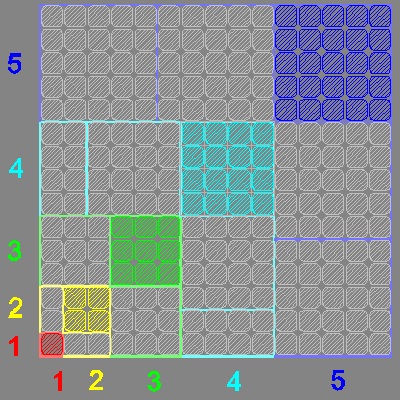
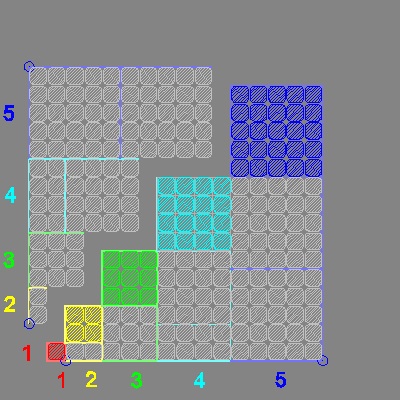
Now let us separate upper left portion of this tile pattern as shown in the left below.
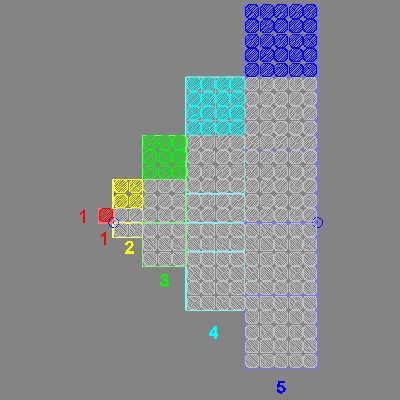
If this is rotated 90 degrees clock-wise, and aligned with the horizontal line,
where numbers 1,2,3,4 & 5 are written ,then we have a staircase like pattern
as shown in the right.
Just as the original square rotated 90 degrees around the red tile 4 times forms a square.
so does the staircase . This will lead to the next visualization scheme.
















*************sumcube_2_1.dwg ************ ************sumcube_2_2.dwg **************


Method 3

Sum of integers cubed from 1 to N arranged in the staircase like pattern(Ref. 3),
which is then copied around 4 times, will form a square.
From the figure it is easy to see
4 x Sum = {N (N + 1)}2.
Therefore Sum = (1/4){N (N + 1)}2.

You can see the process in animation
for N=4 case.


To create this drawing and animation:
  Load sumcube_1.lsp ---> (load "sumcube_1")
  Then from command line, type sumcube_1








*****************sumcube_1_final.dwg *****************

References

  1. Wells, David: The Penguin Dictionary of Curious and Interesting GEOMETRY. London,England: Penguin Books, p.198, 1991.(Out of print)

  2. Conway,J.H., Guy,R.K.: The Book of Numbers. Springer-Verlag,New York, p 27, 1995.

  3. Nelson,R.B. : Proofs Without Words: Exercises in Visual Thinking. MAA,p.85,87, 1993.

  4. Dantzig, Tobias : NUMBER, The Language of Science. New York: The Free Press, p.269, 1930.
Go to   Fun_Math Content Table   Sums of Integers and Series

All comments/suggestions should be sent to Takaya Iwamoto

Last Updated July 9-th, 2006

Copyright 2006 Takaya Iwamoto   All rights reserved. .