Go to Fun_Math Content Table Sums of Integers and Series
Sum of N equally spaced numbers (Arithmetic Progression)
List of animations posted on this page.(Click the text to watch animation.)Triangular number
Sum of integer (1)
Sum of integer (2)
Sum of odd integer (1)
Sum of odd integer (2)
General case of Arithmetic Progression
1. Sum of Natural numbers (I)
It was probably
Pythagoras of Samos(circa 569-475 BC)
who discovered that the sum of
any number of successive terms of the series
of natural number is a triangular number (ref. 3).

************************* triangular_number.dwg *************************
Greek mathematicians knew that two consecutive triangular numbers makes a square pattern.
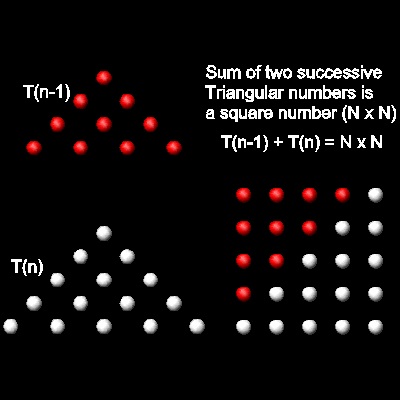
You can see the process in animation for N = 5 case.
So we have the following relation.
Tn-1 + Tn = N2
If N is added to both sides,
(Tn-1 + N ) + Tn = 2Tn = N2 + N = N(N + 1)
To create this drawing and animation:
Load sumtrig.lsp (load "sumtrig")
Then from command line, type sumtrig
Note* : This program requires white_ball.dwg & red_ball.dwg .
*********** sumtrig_final.dwg **************
This result will lead us to the next visual demonstration .
Sum of natural numbers from 1 to N = (1/2) N (N + 1) (ref. 2 ,p.69)
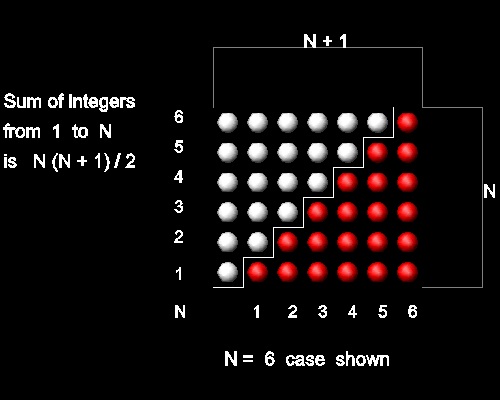 This figure shows that twice the sum of 1 to N is N(N+1), or
This figure shows that twice the sum of 1 to N is N(N+1), or
2 Tn = N (N + 1) . Hence Tn = (1/2) N (N + 1)
You can see the process in animation for N = 6 case.
To create this drawing and animation:
Load sumint_1.lsp (load "sumint_1")
Then from command line, type sumint_1
Note* : This program requires white_ball.dwg & red_ball.dwg .
******************sumint_1_final.dwg ******************
2. Sum of Natural numbers (II)
Another way to look at this is done by rearranging triangular numbers in a "staircase" fashion
and think in terms of "oblong" number.
According to Ref 3, the earliest Pythagoreans discovered
the fact that 'oblong' number is double of a triangular number.
Here 'oblong' number is of the type n(n+1).
 The Greek mathematicians
also knew the connection between oblong numbers and squares,that is,
4 'oblong' + 1 makes a square. The figure in the left shows this fact.
The Greek mathematicians
also knew the connection between oblong numbers and squares,that is,
4 'oblong' + 1 makes a square. The figure in the left shows this fact.
Since one oblong number is made up of 2 identical triangular numbers,
this figure is saying that 8 triangular numbers + 1 = square number.
If a red-tile stair block is merged with a white-tile block in the adjacent
oblong block, it makes a pyramid-like block around one center square.
Then the whole square can now be viewed as being made up of
four of this new blocks instead of the 4 oblong blocks.
This idea will lead us to the next visualization scheme. (Ref. 5)
***********sumint_2_oblong.dwg ***********
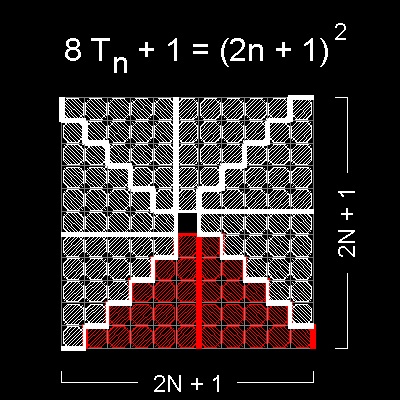 The statement "8 triangular numbers + 1 = square number." is translated into the following formula.
The statement "8 triangular numbers + 1 = square number." is translated into the following formula.
8 Tn + 1 = (2n + 1)2
Hence 8 Tn = (2n + 1)2 - 1 = 4 n(n+1) --> Tn = n(n+1)/2
You can see the process in animation.
To create this drawing and animation:
First, load sumint_2.lsp (load "sumint_2")
Then from command line, type sumint_2
Note* : This program requires white_hatch.dwg .
************sumint_2_final.dwg ************
3. Sum of Odd Natural Numbers (I)
Sum of odd natural numbers from 1 to 2N-1 is N2 as shown in the figure below.
It forms a square, hence this summation is called a "square" number.(Ref 3, 4)
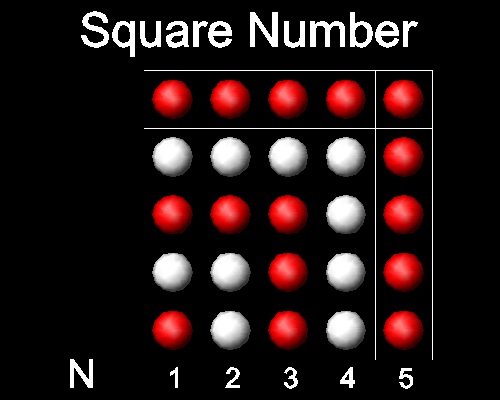
***************** square_number.dwg *****************
(Ref.3):"It is easy to see that,if we have a number of dots forming and filling up a square
(say 16, as in the accompanying figure),the next higher square, the square of 5, can be
formed by adding rows of dots round two sides of the original square as shown.
The number of so added is 2.4 + 1 = 9. This process of forming successive squares can be
applied throughout,beginning from the first square number 1. The successive numbers added
to the 1 are, as shown in the next figure,3, 5, 7, .....(2n+1),
that is to say,the successive odd numbers.
The method of formation shows that the sum of any number of successive terms of the series
of the odd numbers 1,3,5,7 ....(starting from 1) is a square, and in fact
1 + 3 + 5 + ....+ (2n - 1) = n2,while the addition of the next odd number (2n + 1) makes
the next higher square, (n+1)2. All this was known to Pythagoras."
Note that N2 + 2N + 1 = (N + 1)2
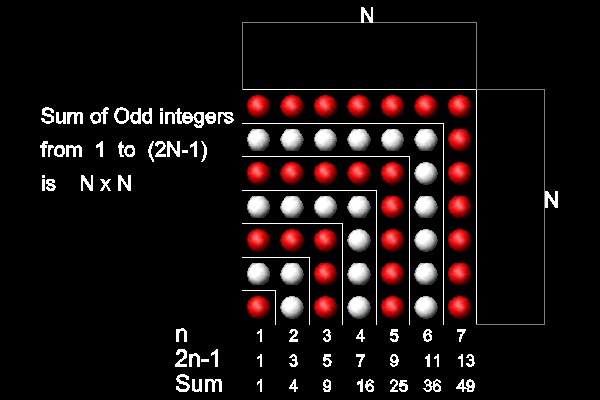
You can see the process in animation
for N=7 case.
To create this drawing and animation:
Load sumodd_1.lsp (load "sumodd_1")
Then from commnad line, type sumodd_1
This program requires red_ball.dwg & white_ball.dwg.
************************sumodd_1_final.dwg ************************
Now move the upper diagonal section to the left as shown in the figure below,
and rotate 90 degrees clock-wise to form a triangle in the right.
From left to right , the sequence is still 1, 3, 5, ... , odd numbers.
This will lead us to the next visualization scheme.
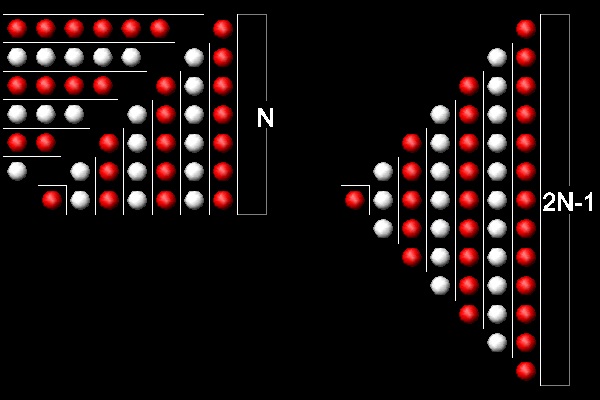
************************sumodd_1_a.dwg ************************
4. Sum of Odd Natural Numbers (II)
Sum of odd integers from 1 to 2N-1 is N2 as shown in the figure below.(ref 2. p.72)
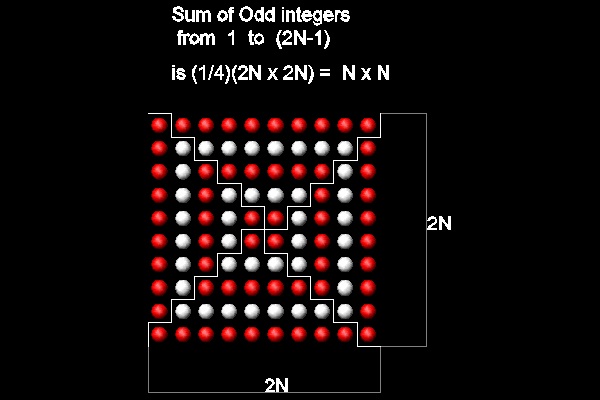
You can see the process in animation
for N=5 case.
To create this drawing and animation:
Load sumodd_2.lsp (load "sumodd_2")
Then from command line, type sumodd_2
This program requires red_ball.dwg & white_ball.dwg.
************************sumodd_2_final.dwg ************************
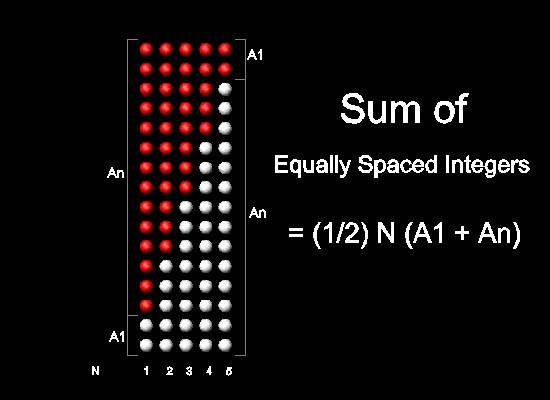
5. Generalization: Sum of N equally spaced numbers
(Ref.1)The arithmetic progressions discussed above can be treated as special cases of sum of N equally spaced numbers.
N equally spaced arithmetic progression is defined as follows:
An = A1 + N x d, where d is a constant number, and N=1,2,3,....
When A1 = 1, then d=1 is the natural number , and d=2, odd numbers.
In general, A1 and d are real numbers. They need not to be integers.
Then the sum of first N terms is Sn = (1/2)N(A1 + An)
Examples:
Sum of 1,2, 3, ..., N = (1/2)N(A1 + An) = (1/2)N(1 + N)
Sum of 1,3,5,..(2N-1) = (1/2)N(A1 + An) = (1/2)N{1 + (2N-1)} = (1/2)N*2N = N2
 You can see the process in animation
You can see the process in animation
for A1=2, d = 3, N = 5 case.
To create this drawing and animation:
Load sumint_3.lsp (load "sumint_3")
Then from command line, type sumint_3
This program requires red_ball.dwg & white_ball.dwg.
*************arithmetic_progression_final.dwg *************
References
- Conway,J.H., Guy,R.K.: The Book of Numbers. Springer-Verlag,New York, p.33, 1995.
- Nelson,R.B. : Proofs Without Words: Exercises in Visual Thinking. MAA, p.69, 1993.
- Heath, Sir L.H.: A manual of Greek Mathematics. Dover Edition ,p.43, 1963. Originally published in 1931.
- Wells, David: The Penguin Dictionary of Curious and Interesting NUMBERS. London,England: Penguin Books, p.85, 1986.
- Wells, David: The Penguin Dictionary of Curious and Interesting GEOMETRY. London,England: Penguin Books, p.198, 1991.
- Dantzig,Tobias: NUMBER, The Language of Science. New York: The Free Press, p.41-43, 1930.