*********** square_number.dwg ***********
Go to Fun_Math Content Table Sums of Integers and Series
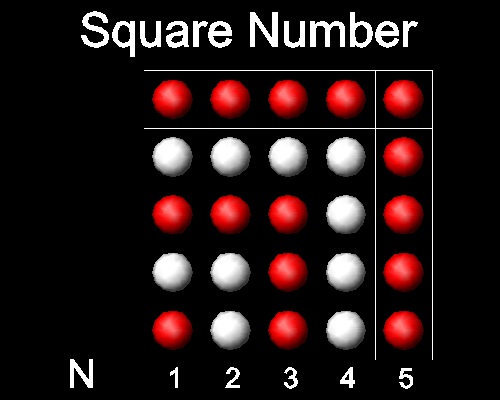
Sum of odd natural numbers from 1 to 2N-1 is N2 as shown in the figure below.
It forms a square, hence this summation is called a "square" number.

*********** square_number.dwg ***********
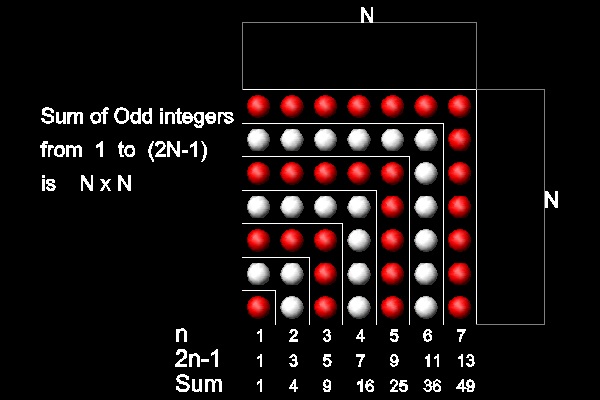
(Ref.1):"It is easy to see that,if we have a number of dots forming and filling up a square (say 16, as in the accompanying figure),the next higher square, the square of 5, can be formed by adding rows of dots round two sides of the original square as shown. The number of so added is 2.4 + 1 = 9. This process of forming successive squares can be applied throughout,beginning from the first square number 1. The successive numbers added to the 1 are, as shown in the next figure,
3, 5, 7, .....(2n+1), that is to say,the successive odd numbers. The method of formation shows that the sum of any number of successive terms of the series of the odd numbers 1,3,5,7 ....(starting from 1) is a square, and in fact
1 + 3 + 5 + ....+ (2n - 1) = n2,while the addition of the next odd number (2n + 1) makes the next higher square, (n+1)2. All this was known to Pythagoras."
Note that N2 + 2N + 1 = (N + 1)2
*****************sumodd_1_final.dwg *****************
You can see the process in animation.animation
Executables for creating this drawing and animation:
Load sumodd_1.lsp ---> (load "sumodd_1")
To execute: from command line: sumodd_1
All questions/complaints/suggestions should be sent to takaya.iwamoto@comcast.net
Last Updated July 9-th, 2006
Copyright 2006 Takaya Iwamoto All rights reserved.