Go to Fun_Math Content Table
Sums of Integers and Series
Sum of integers squared
List of animations posted on this page.(Click the text to watch animation.)
Relation between Tetrahedral and Triangular numbers
Sum of squares vs. Triangular numbers
3D cube animation for sum of squares
Tetrahedral number and Pyramid number
Sum of integers squared from 1 to N is also called "Square Pyramid Numbers" because each layer of the balls
makes a square pattern.
It is expressed as Pyrn = 12 + 22 + 32 + ... + N2
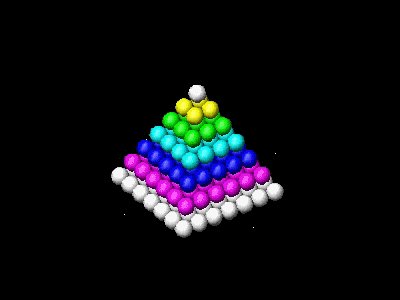
Instead ,if the cross section pattern is a triangle, then it makes the following number sequence.
1 = T1 = 1
1 + (1 + 2) = T1 + T2 = 4
1 + (1 + 2) + (1 + 2 + 3) = T1 + T2 + T3 = 10
1 + (1 + 2) + (1 + 2 + 3) + (1 + 2 + 3 + 4) = T1 + T2 + T3 + T4 = 20
and so on.
This is the sum of the Triangular number,i.e. Tetn = T1 + T2 + T3 + .... + Tn
This number is called Tetrahedral number.
It has been shown already that two consecutive triangular numbers makes a square number. Analogous rule exists for
square pyramid,i.e.,a square pyramid is made up of two consecutive tetrahedral numbers.
This relation between Square_Pyramid number and Tetrahedral number is easily understood by looking at the next two figures.
The figure below shows that One pyramid number is made up of two tetrahedral numbers, in this example
Pyr5 = Tet4 + Tet5
and in general, Pyrn = Tetn-1 + Tetn
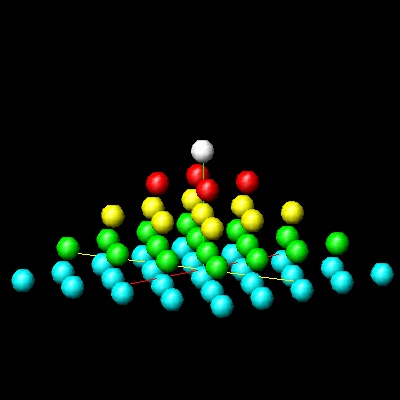
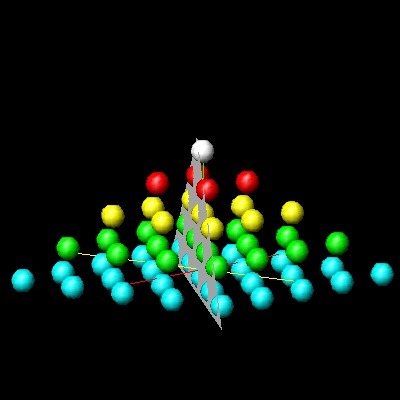
********square_pyramid_final.dwg *******
********square_pyramid_cut.dwg *******
To create this drawing :
Load sumsqr_1.lsp (load "sumsqr_1")
Then from command line, type square_pyramid
Spacing is chosen to be 2.0~2.5 . Closely packed when 1.5 .
The center plane is drawn by the command : cut_plate
Note* : This program requires
red_ball.dwg ,yellow_ball.dwg ,green_ball.dwg ,cyan_ball.dwg
blue_ball.dwg ,magenta_ball.dwg ,white_ball.dwg.
(Ref.1 p.45) shows a very interesting visual proof that the formula for n-th tetrahedral number is
Tetn = (1/6) n(n+1)(n+2)
by using Triangular numbers.
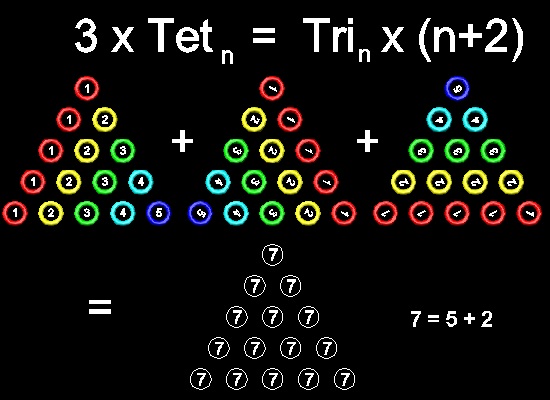
The details of process can be seen in running animation for N=5 case.
To create this drawing and animation:
Load sumsqr_3.lsp (load "sumsqr_3")
Then from command line, type sumsqr_3
Note* : This program requires
red_1_ring.dwg ,yellow_2_ring.dwg
green_3_ring.dwg ,cyan_4_ring.dwg
blue_5_ring.dwg ,magenta_6_ring.dwg
white_7_ring.dwg.
*********************sumsqr_3_final.dwg *********************
In the figure;
Upper row --the first triangle : Tet5, and Tn on its n-th row.
Upper row --the second triangle : rotate the first triangle 120 deg. clockwise using top apex as pivot .
Upper row --the third triangle : rotate the second triangle 120 deg. clockwise using top apex as pivot .
Lower row: adding all numbers in the circles at the same locations.Note that the total number of circles
are 5-th Triangulaer number(Tsub>5 = 1 + 2 + 3 + 4 + 5 )
So what this picture tells us is 3 x Tet5 = T5 x (5 + 2).
And in general, 3 x Tetn = Tn x (n + 2) = (1/2)n (n + 1) (n + 2)
Then finally, Tetn = (1/6) n(n+1)(n+2)
Now the Pyramid number can be expressed as follows.
Pyrn = Tetn-1 + Tetn = (1/6)(n-1)n(n+1) + (1/6)n(n+1)(n+2) = (1/6)n(n+1)(2n+1)
1. Sum of integers squared (Planar Approach)
Ref.1 shows a planar approach using two facts already shown in the previous sections,i.e.
1. Adding consecutive triangular number makes a square,or Tn-1 + Tn = n2 .
2. Triangular number : Tn = (1/2)n(n+1)
 You can see the process in animation.
You can see the process in animation.
To create this drawing and animation:
Load sumsqr_2.lsp (load "sumsqr_2")
Then from command line, type sumsqr_2
************sumsqr_2_final.dwg ***********
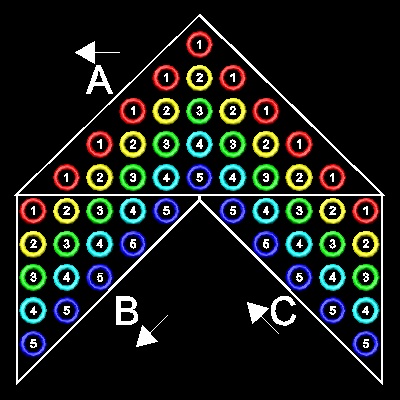
The example shown is for N=5 case. At the center line, draw a column of T5.
Then make N (= 5) copies of the Tn at both sides as shown.
Total number of columns is (2N + 1) (= 11).
Next, make three groups A, B, & C as shown.
Sums of numbers in 3 groups are done in the arrow direction in the figure.
Group A: Starting from top , 1 , 1+2+1, 1+2+3+2+1, 1+2+3+4+3+2+1,... Since each term is a sum of two consecutive
Triangular number, each term is a number squared. Sum of these Sn=1+22+32+42+52.
Group B: 1+22+32+42+52. So this is the sum of integer squared (Sn)
Group C: The same as group B. Sum is Sn.
So we have (2N+1) copies of Trianglar number Tn, and three groups of sum of integer squared.
Therefore 3 Sn = (2N+1)Tn = (2N +1)N(N+1)/2
or Sn = (2N +1)N(N+1)/6
2. Sum of integers squared (3 Dimensional Approqach)
But the one shown in Ref.2 seems to be the best from the visualization point of view.
The following figures are the early and the final steps.
The details of process can be seen in running animation for N=5 case.
******* 3 identical blocks arranged parallel to x,y & z axes are assembled into one block.*******

 ***************sumsqr_1_start.dwg **************
***************sumsqr_1_final.dwg **************
***************sumsqr_1_start.dwg **************
***************sumsqr_1_final.dwg **************
The volume of the final block is N(N+1){N+(1/2)} as shown above.
Since it is made up of three blocks, each of which is sum of squares 1 + 22+ 32+ ...+ N2,
3 (1 + 22+ 32+ ...+ N2) = 3 Sn = N(N+1){N+(1/2)} ,or
Sn = (1/6)N(N+1)(2N+1)
To create this drawing and animation:
Load sumsqr_1.lsp (load "sumsqr_1")
Then from command line, type sumsqr_1
Author's note:With some unknown reason, the program comes to a halt after 3 blocks are put together.
To continue the process, the following lines must be typed in the command line window.
explode
!ss3
hit return key
finish_up
Note* : This program requires
red_cube.dwg ,yellow_cube.dwg ,green_cube.dwg ,cyan_cube.dwg
blue_cube.dwg ,magenta_cube.dwg ,white_cube.dwg.
References
- Conway,J.H., Guy,R.K.: The Book of Numbers. Springer-Verlag,New York, p 27, 1995.
- Nelson,R.B. : Proofs Without Words: Exercises in Visual Thinking. MAA, p.77, 1993.
Go to
Fun_Math Content Table
Sums of Integers and Series
All questions/suggestions should be sent to Takaya Iwamoto
Last Updated Sept 9-th, 2006
Copyright 2006 Takaya Iwamoto All rights reserved.
.
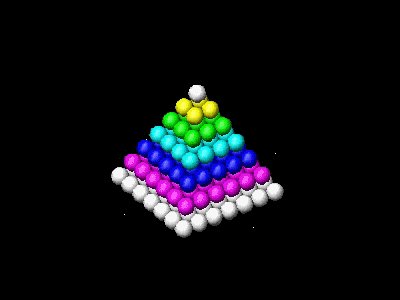



 You can see the process in
You can see the process in 
 ***************
***************