Doubling the Cube
Go to   Fun_Math Content Table   Three Famous Problems   Delian Problems

Later Mathematicians

1. Nicomedes revisited

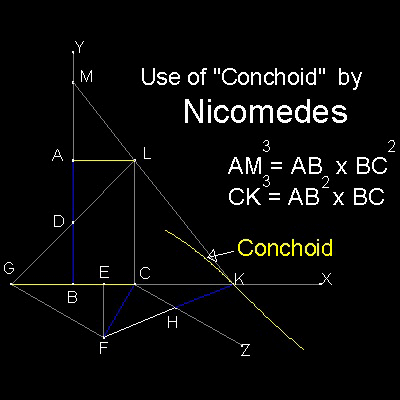
The central issue of Nicomedes's solution is finding point "K" by neusis process (verging) across line CZ and CX.

The data of the two given line segments are implied by BC and CF (= AD = HK).

Since AM = FH, all the elements needed in the argument are included in the figure made up of points B,C,E,F,G,H,K,and Z .

Figures associated with points A,L,D,M looks redundant !!
********* Nicomedes_Delian_desc.dwg ********

Later mathematicians (I do not know who.) noticed this and modified Nicomedes' Delian model as follows:
Draw a line FB. Extend it to point V, such that BV = BF (= CF = AD).
Connect V and C.
Then points V,C,H and Z are on a line VZ.
Why ?-- Show that angle FCV is 90 degrees.
Extracting only the lower part of Nicomedes' model, it looks like the figure below.


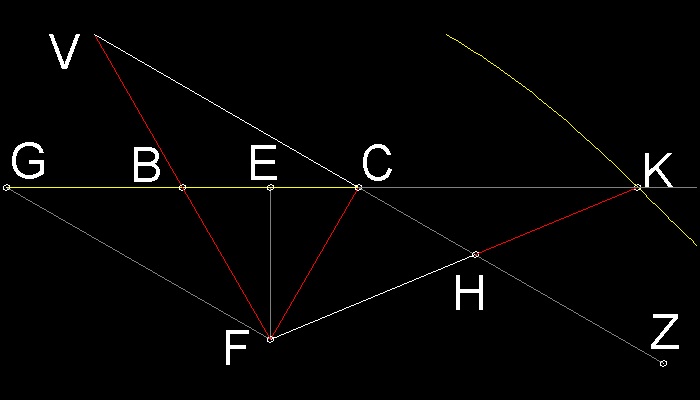
**************************** Nicomedes_modified.dwg **************************

Line FG is not required anymore,because line CH is now be drawn by line VZ.
Eliminating line GF and point G, and making a mirror image of the whole picture with reference axis BC,
the model now looks like the figure shown below.


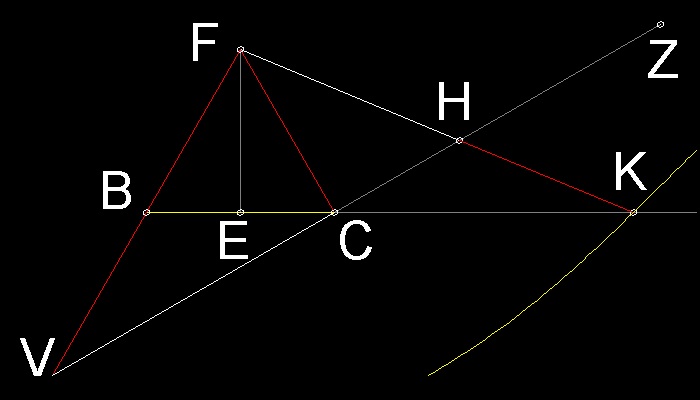
*************************** Nicomedes_modified_a.dwg ************************

Now 2 models,which are slightly different in line length BC definition, are shown in Ref. 1 and 2.

They are chosen here because both comes with very interesting proofs.

General case (Ref.2)

Names for the points are changed to match those of ref.2 for easier referencing.
In the drawing , length AB = (k / 4) , where 0 < k < 8 .
Line CE is drawn parallel to BA.
Objective of the process is to find point S such that RS = 1.
Then , x = (k)1/3


*************************** Nicomedes_modified_b.dwg ************************
Summary of the proof (Ref.2) 

 
 Since B is a midpoint of CD ,and AB is parallel to CE, CE = 2 AB = k / 2 
 Also since triangle ECR and ASR are similar,
 we have  (k/2) / CR = AS / 1.
 If we let AS = x, 	then CR = k/(2x) 					(1) 
 Using Pythagorean theorem twice, we now have
 	CS2 = [1 + k /(2x)]2 = CM2 + MS2 = [CB2 - BM2] + MS2
				 = [12 - (k/8)2] + [x + (k/8)]2
 Rearranging x terms according to its power, the result will be a following quartic equation.
 	4x4 + kx3 - kx - k2 = 0
 This equation canbe factorised as follows:
	(4x + k)(x3 - k) = 0
 Since (4x + k) > 0, we have  x3 - k = 0

 Therefore  x = (k)1/3 							(2)
 Substituting (2) into (1) , we get
	y = CR = (1/2)k2/3							(3)
 When ABC is an equilateral triangle, k = 4.
 Then from (2) and (3), BS( x ) and CR ( y ) become
		x = BS = (2)2/3
		y = CR = (2)1/3
	
 This k = 4 case is the next model (ref. 1).

Equilateral Triangle case (Ref.1)

This is the case when ABC is an equilateral triangle case.
So in the drawing below, AB = BC = CA = k.
The process is to draw a line CP such that QP = k.
Then, CQ = k (2)1/3 and BP = y = k (2)2/3


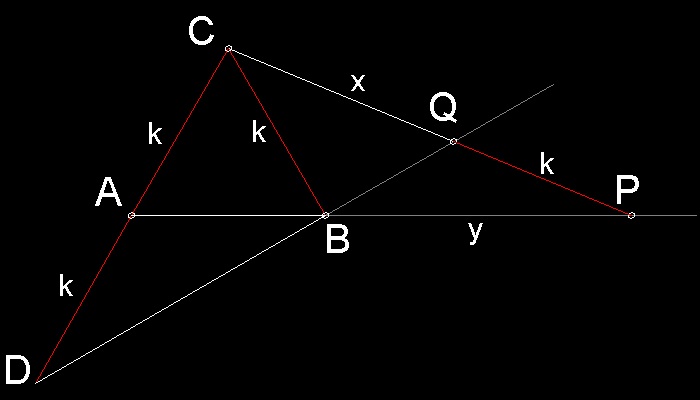
* ************************** Nicomedes_modified_c.dwg ************************

Ref.1 gives a very interesting proof instead of the proof for a general case above.

It uses 2 famous theorems in geometry.One is by Menelaus, and the other is Proposition 36, in Book III of Euclid.
The latter is called "the leg transversal theorem" in Ref.1 .
They are shown in the drawing below.


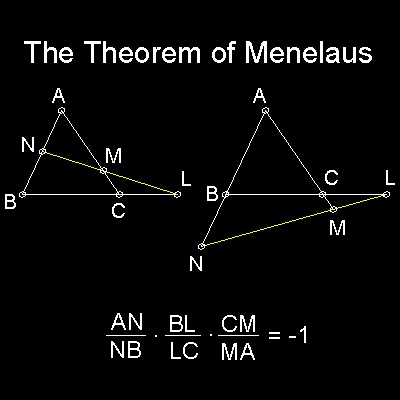
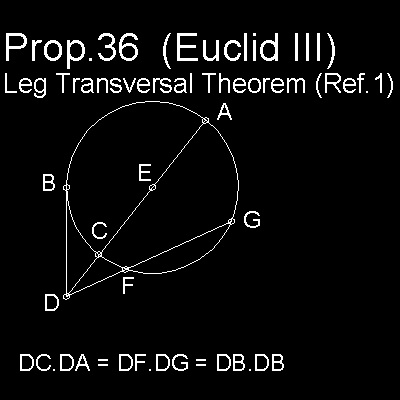
*********** Menelaus_theorem.dwg *********** ********** transversal_theorem.dwg **********

Proof given in Ref.1 . 

 
 Preliminaries:
   The equation of two mean proportionals between 2k and k is given by
	2k/y = y/x = x/k
   So we have three curves.
	parabola-1	y2 = 2kx					(i)
	parabola-2	x2 = ky					(ii)
	hyperbola	xy = 2k2					(iii)

   If (1) and (ii) are combined, we have a circle equation.
	circle		x2 + y2 -2kx -ky = 0			(iv)

   The intersection of (i) and (iv) gives the Delian solution.
   The following proof use this idea.
	
 (I)  When the theorem of Menelaus is applied to triangle ABC,with line DBQ
      traversing,
 	AD.CQ.BP = PQ.AB.CD or
		xy = 2k2							    	 (1)
 (II) In the Prop. 36 picture,
		DF.DG = DC.DA = (DE - CE)(DE + CE) = DE2 - CE2	     	 (2)
      Now,imagine a circle with its center at point C, and radius k.
	(2) will be written as
		PB.PA = PC2 - k2 or
		y (y + k) = (x + k)2 - k2 = x2 + 2kx 		  		 (3)

	
Proof in Ref.1 stops here stating that (1) represents the hyperbola,and (3) is a circle equation equivalent
to 2 parabolas.Hence the solution of (1) and (3) is the Delian solution.
      Now let us proceed to obtain the solution.
	
      Substituting (1) into (3), the equation will be written as
		(2k + x)(x3 - 2k3) = 0
      Since (2k + x) > 0, we have
		x3 - 2k3 = 0					  			 (4)
      Therefore,
		x = k (2)1/3

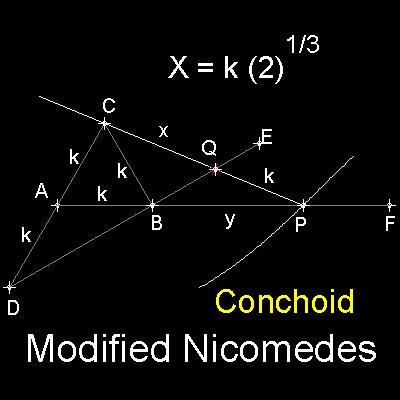
ABC is an equilateral triangle with side length k.
Extend CA and at distance k from A, make point D.
Draw a line from D through B to point E.
Draw a line from A through B to point F.
Draw a line through point C,intersecting line BE at Q,
and intersecting line AF at P such that PQ = k.

Then CQ = k (2)1/3

In order to find point P,
a ruler with two markers with distance k apart

,or a curve called Conchoid
(C as "pole", BE as "rule", and k as "distance") can be used.
******** modified_Nicomedes_desc.dwg *******

For detail, go to the section Nicomedes - Revisited.

References

1. Dorrie,Heinrich: "100 Great Problems of Elementary Mathematics",English translation, Dover, 1965.Original published in German in 1932

2. Martin,George E.: "Geometric Constructions",Undergraduate Texts in Mathematics,Springer Verlag,1997.

3. Descartes,Rene: "The Geometry of Rene Descartes",original in French and Latin, English Translation, Dover, 1925.

Go to   Fun_Math Content Table   Three Famous Problems   Delian Problems

All questions/suggestions should be sent to Takaya Iwamoto

Last Updated Nov 22, 2006

Copyright 2006 Takaya Iwamoto   All rights reserved. .