Squaring the Circle
Go to   Fun_Math Content Table   Three Famous Problems   Greek Circle Squarer   Later Squarer

Later Circle Squarers

René Descartes

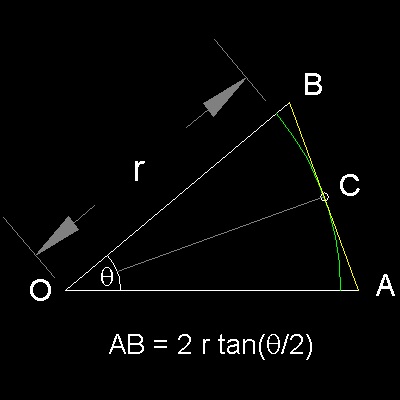
René Descartes (1596 - 1650) ,the famous founder of analytical geometry, also used polygon approach to determine the value of p. But instead of computing the perimeters of polygons inscribing (and/or) circumscribing a given circle, he kept the perimeter length constant, and doubled its sides until the polygon approaches the circle. 

 
 From the figure, the perimeter of the n-sided
 polygon (L) is
	L = n.AB = 2 n r tan(q/2)			(1)
 Then after doubling the sides k times ( 2k)
	L = 2 n 2k r tan((q/2)/2k)	
	  = n r 2k+1	tan(q/2k+1)			(2)
 Descartes started from n = 4, and q= p/2
 So 	L = 4 r 2k+1	tan((p/2)/2k+1) 
	  = (2r) 2k+2 tan(p/2k+2)
 Dividing both sides by 2r(Diameter), we get
	L/(2r) = 2k+2 tan(p/2k+2)			(3)
 The left hand side is the ratio of 
 perimeter to diameter.
 Therefore as k becomes large, 
 this will approach the value of p.
 Or p is a limit value of  2k+2 tan(p/2k+2)	(4)

******** Descartes_pi_model_base.dwg ********

Graphical solution of René Descartes


******** Descartes_circle_square_model.dwg ******** 

 
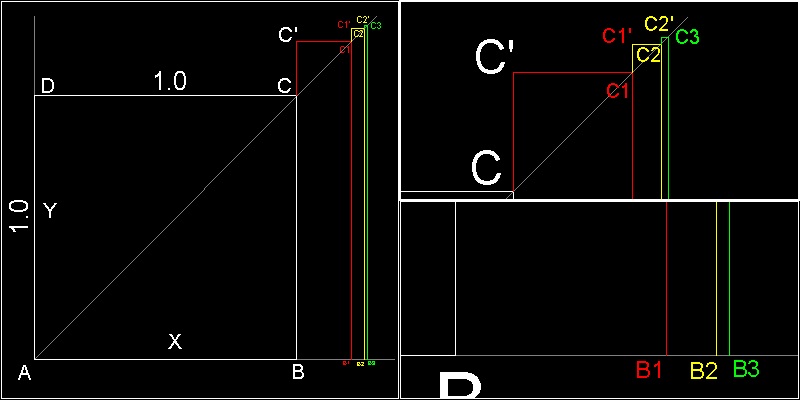
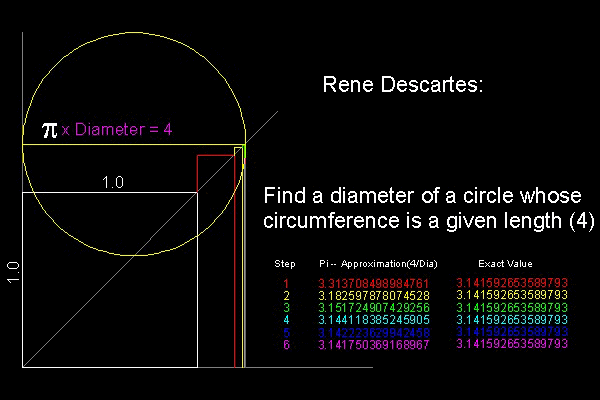
 From (3)
	xk = 2r = (L/2k+2)cot(p/2k+2)		(5)
 Descartes noticed that (5) is the positive root of the
 following recursive equation.
	xk(xk - xk-1) = x02/4k			(6)
 where L = 4x0
 When xk-1 is given, this is a quadratic equation with respect to xk.
 This can be verified by substituting Xk, and xk-1 expressed
 in terms of cot(q) into (6)  and using the double angle 
 formula for cotangent,i.e.
		cot(2q) = (cot2q - 1)/(2 cotq)

 The graphical interpretation of (6) is as follows:
 Start with a square ABCD  with a unit side length.
 Find points B1,C1 such that area B B1 C1 C' is 1/4 of the area of the square.
 Next find points B2, C2 which makes the area B1 B2 C2 C1' equal to 1/4 of rectangle B B1 C1 C'.
 And so on ...

 During the process, length ABi, where i = 1,2,3,...., is the diameter of the circumscribing polygon
 which makes the perimeter value the constant (4 x0).
 Therefore the estimated value of p at that level of side doubling is obtained
 by dividing 4 by this diameter value.

Result of René Descartes


***************** Descartes_circle_square_desc.dwg *****************

To create this drawing :
   Load Descartes_pi.lsp    (load "Descartes_pi")
  Then from command line, type Descartes_pi 

 
    	The result of this program is shown below:
	15-th decimal place is correct after 25-th step.
 
      step	Approximate value
	
	1 	3.31370 84989 84761
  	2 	3.18259 78780 74528
  	3 	3.15172 49074 29256
  	4 	3.14411 83852 45905
  	5 	3.14222 36299 42458
     	6 	3.14175 03691 68967
  	7 	3.14163 20807 03182
  	8 	3.14160 25102 56809
  	9 	3.14159 51177 49589
  	10 	3.14159 32696 29307
     
	11 	3.14159 28075 99644
   	12 	3.14159 26920 92255
  	13 	3.14159 26632 15408
  	14 	3.14159 26559 96197
  	15 	3.14159 26541 91394
   	16 	3.14159 26537 40194
  	17 	3.14159 26536 27393
  	18 	3.14159 26535 99193
	19 	3.14159 26535 92143
 	20 	3.14159 26535 90380
    
	21 	3.14159 26535 89939
	22 	3.14159 26535 89829
 	23 	3.14159 26535 89801
 	24 	3.14159 26535 89795
  	25 	3.14159 26535 89793	 --> Correct to 15-th decimal place

References

Go to   Fun_Math Content Table   Three Famous Problems   Greek Circle Squarer   Later Squarer

All questions/suggestions should be sent to Takaya Iwamoto

Last Updated Feb 17,2007

Copyright 2006 Takaya Iwamoto   All rights reserved. .