************* Snell_Huyg_lb.dwg ************* ************* Snell_Huyg_ub.dwg ************
Willebrord van Royen Snell (1580 - 1626),
who is today known for his discovery of the law of reflection and refraction, was a student of
Ludolph van Ceulen (1540 - 1610)
at the University of Leyden.
Ludolph took the same method Archimedes used almost 19 centuries ago, and computed the value of π up to 35-th decimal place
using 262 -sided polygon ,inscribed and circumscribed.
Snell searched for better lower and upper bounds so that the value of π can be computed using less number of sides of polygon.
And he found the following sets. Although he could not prove the proposition (which was later done by
Christiaan Huygens (1629 - 1695))
, he used this result to verify Ludolph's 35-th decimal place using only 230-sided polygon.
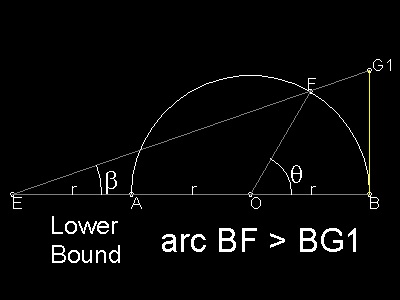
lower bound: Refer to the drawing below-left.
Make EA equal to the radius ( r ) ,where E is on AB extended.
Select any point F on the circle, and let G 1 be the intersection of EF and the tangent at point B. Then
arc BF > BG1
As mentiond above , this is the approximation of π derived by Cardinal Nicholas Cusanus(1401-1464).
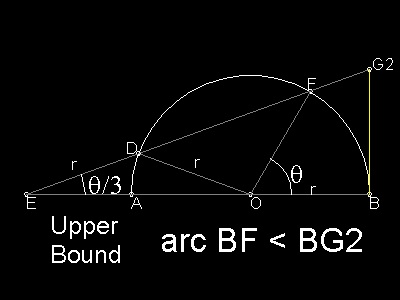
upper bound: Refer to the drawing below-right
Choose a point D on a circle. Make DE equal to its radius r, where E is on AB extended.
The extension of DE intersects the circle at point F, and at point G2 with tangent erected at B. Then
arc BF < BG2
Note here that we started from point D, then find out point F as an intersection DE and the referenced circle..
If we started at F, then the finding point D becomes a "Trisection" problem..


************* Snell_Huyg_lb.dwg *************
************* Snell_Huyg_ub.dwg ************
To create these drawings:
Load pi_approximation.lsp (load "pi_approximation")
Then from command line, type Snell_Huygens_LB for lower bound drawing.
And from command line, type Snell_Huygens_UB for upper bound drawing.
Referenced drawing: Snell_Huygens_lb.dwg
BG1 : representing the half the side-length of the circumscribing polygon
BG1 = 3r tan b (1)
In triangle EOF:
Sine law : EF/(sin(π-θ) = r / sin β (2)
Cosine law: EF2 = EO2 + FO2 - 2EO*FO*cos (π-θ)
=(2r)2 = r2 + 2*2r*r*cos θ
=5 r2 + 4r2cos θ
Therefore EF = r (5 + 4cos θ)1/2 (3)
Substituting (3) into (2),
sin β = sin θ / (5 + 4cosθ)1/2 (4)
Using the equality cos β = 1 -sin2 β,
cos β = (cos θ + 2)2 / (5 + 4 cos θ)1/2
Then tan β = sin θ / (2 + cos θ)
Finally ,
BG1 = 3 r sin θ /(2 + cos θ)
|
Referenced drawing: Snell_Huygens_ub.dwg Length ED is set equal to r. Note that angle DEA = θ / 3, and this is exactly the same configuration Archimedes used for trisecting the given angle θ. EO = 2r cos(θ/3) BG2 = EB*tan(θ/3) = (EO + r*tan(θ/3) = r(2 cos(θ/3) + 1) tan(θ/3) |
What Snell found and were later proved rigorously by Huygens is summarized as follows:
BG1 < arc BF < BG2
or
3 r sin θ /(2 + cos θ) < r θ> < r {2 cos(θ/3) + 1} tan(θ/3)
Starting with a hexagon , and after doubling the number of sides of ploygon
k times (i.e. 2k times) ,this inequality can be written as follows:
6 x 2k x 3 sin α /(2 + cos α) < π < 6 x 2k(2 cos(α/3) + 1) tan(α/3)
where, α = θ / 2k = (π/6)/2k
A simple program is run to check the efficency of these limits.
Load the program "pi_approximation.lsp", and run typing Snell_pi in the command line window.
The result are given below.
** k ** Lower bound : Upper bound
error LB - π : UB - π
** 0 ** 3.14023 73433 66169 : 3.14174 00162 53954
error 0.00135531 : 0.000147363
** 1 ** 3.14150 99936 42921 : 3.14160 17882 54884
error 8.26599e-005 : 9.13467e-006
** 2 ** 3.14158 75188 57949 : 3.14159 32233 40417
error 5.13473e-006 : 5.69751e-007
** 3 ** 3.14159 23331 59636 : 3.14159 26891 81042
error 3.2043e-007 : 3.55912e-008
** 4 ** 3.14159 26335 70565 : 3.14159 26558 13962
error 2.00192e-008 : 2.22417e-009
** 5 ** 3.14159 26523 38710 : 3.14159 26537 28799
error 1.25108e-009 : 1.39006e-010
** 6 ** 3.14159 26535 11601 : 3.14159 26535 98480
error 7.81912e-011 : 8.68772e-012
** 7 ** 3.14159 26535 84905 : 3.14159 26535 90335
error 4.8872e-012 : 5.42233e-013
** 8 ** 3.14159 26535 89487 : 3.14159 26535 89826
error 3.05533e-013 : 3.37508e-014
** 9 ** 3.14159 26535 89774 : 3.14159 26535 89794
error 1.86517e-014 : 1.77636e-015
The result for hexagon is better than Archimedes' 96-sided polygon case ,
and Snell's 96-sided case gives the correct number up to 6-th decimal place .
He went further to verify his teacher's (Ludolph) work up to 35-th decimal place.
|
Some of Huygens result to be added here. |
All questions/suggestions should be sent to Takaya Iwamoto
Last Updated July 15, 2012
Copyright 2006 Takaya Iwamoto All rights reserved.