ホームページの内容目次に戻る 古代ギリシャ数学の三大問題
円積問題の歴史
問題の定義:
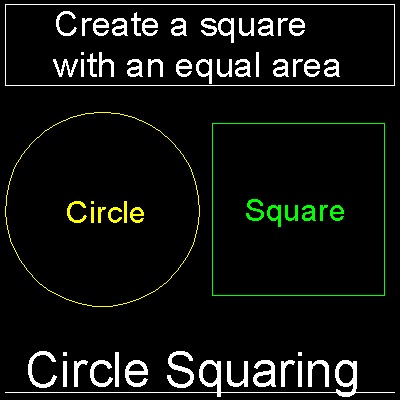
円と同じ面積を持つ正方形を作る。
これは辺の長さが p
の正方形または平方根を作るのに等しい。
******** circle_squaring_problem.dwg
*********
問題の原点:
円は最も単純で人が一番最初に作り出したものである。歴史においても、初めの頃から人は自然に円の面積や円周について非常に関心を持った。
ゲームのルール(Platonian Rule):
使用するツール
コンパスと、目盛りの無い真っ直ぐな辺 。
次の2つのツールは使って良い
1. 二点を通る不定長の直線の図面。
2. ある一点(第一点)を中心とし、与えられた点(第二点)を通る円の構成。
初期の試み:
不可能の証明:
1880年、リンデマン(Ferndinand
von Lindemann, 1852 - 1939) は、p
は超越的で有理係数を持ついかなる多項方程式の根でない、ことを証明した。 そして彼は定規とコンパスでは円を四角化できないことを証明した。
参考文献のコメント:
ホームページの内容目次に戻る 古代ギリシャ数学の三大問題
質問、問い合わせは 筆者 岩本 卓也宛てにお願いします。
Last Updated Nov 22, 2006
Copyright 2006 Takaya Iwamoto All rights reserved.

