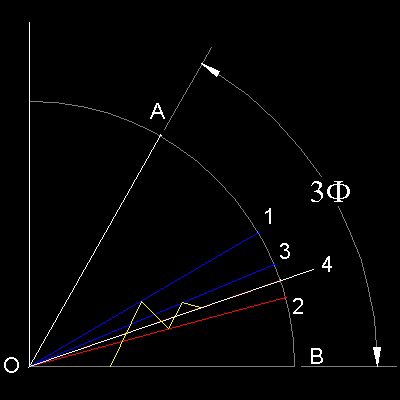
この近似法は、次の幾何級数の和の性質を利用する。
Sn= 1/4 + (1/4)2 + (1/4)3+ (1/4)4+ . . . + (1/4)n
n が増加すると、この級数の和 Sn は 1/3 に近似する。
実際の三等分法は角の二等分の繰り返しである。
例えば、 1/4 = 1/2 - 1/4, (1/4)2 = (1/4){(1/2) - (1/4)}, 等。

三等分する角を∠AOBとする。
n=1 ;∠AOB を二等分(点 1)
n=2 ;∠1OB を二等分(点 2)--∠2OB = 1/4
n=3 ;∠1O2 を二等分(点 3)
n=4 ;∠3O2 を二等分(点 4)--∠4Ob = 1/4 + (1/4)2
n=5 ;∠3O4
n=6 ;更に二等分 ...繰り返す
ここをクリックしてアニメーションを見る。
****** approximation_series_tri_desc.dwg ******
この図面とアニメーションの作成方法:
プログラム gen_sect.lsp を (load "gen_sect") でロードする。
次にコマンド ラインから trisect_by_series と実行命令をタイプする。
アニメーションファイルの作成: animation_series
この近似解は15世紀のドイツの枢機卿(ローマ教皇の最高顧問)であった
ニコラス・フォン・クサ(Nicholas von Cusa 1401-1464)
と16世紀のオランダの数学、物理学者
スネル (Willebrord van Royen Snell 1580-1626)
の功績である。
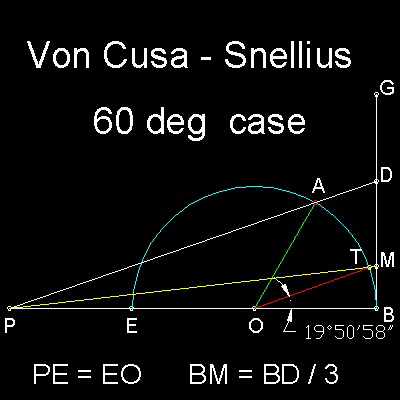
半円OBEを描く。PE = EOとなるBE の延長線上の点P を指定。
半円上の点A を指定し、∠AOB を三等分する角とする。
点B からEB に垂直な線GB を引く。
点P からA を通り、GB と交差する線を引き、その交点をD とする。
線BD 上でBM = BD/3 となる点M を求める。
P と M を繋ぐ。これが点T で半円に交差する。
線分TO が∠AOB の近似三等分線となる。
角度60度の場合、誤差は約9'02"(9分02秒)で、非常に良い結果である!!
******** VonCusa_Snellius_desc.dwg *********
この図面とアニメーションの作成方法:
プログラム VonCusa.lsp を (load "VonCusa") でロードする。
次にコマンド ラインから VonCusa と実行命令をタイプする。
デューラー(Albrecht Dürer 1471-1528)
は画家として有名であるが かれは 数学と絵画の関係について
次のような 意見をもっていた。
"--これからの新しい芸術は科学的でなければならない。 特に 数学こそは 科学のなかでも最も正確で、
論理的で、視覚的に構築できるからである。"
1525年にデューラーは角の三等分に関し、簡単で且つ非常に正確な近似法を発表した。

∠AOB を三等分する角とする。
QA = QB = 1 で M1 と M2 は線分AB を三等分する。
M1 と M2からAB に垂直で弧C1 とC2 と交差する線分を引く。
AD = AC1 となる点D を求める。 \\\\\\
DE = M1D/3 となる点E を求める。
中心をA とし、半径が AE の円を描く。この円は点T で弧と交差する。
線分TO は∠AOB の近似三等分である。
************** Durer_desc.dwg ***************
この図面とアニメーションの作成方法:
プログラム Durer.lsp を (load "Durer") でロードする。
次にコマンド ラインから Durer と実行命令をタイプする。
この簡単な近似法は1928年に Karajordanoff が発見した。
Karajordanoff が如何なる人物であるかについて 調べてみたが 今のところよく分からない。
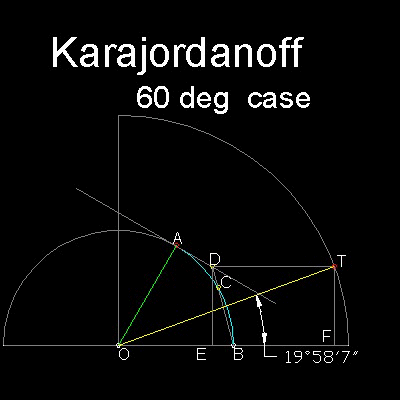
∠AOB を三等分する角とする。
∠AOB に関し、半径1 と2 の二つの円を描く。
点B から弦AB の中点C を通る線を引く。
点A に接線を引く。
この接線と線分BC の延長線が交差する点をD とする。
OB に平行な線DT を引く。この線が外円弧と交差する点をT とする。
線分TO は近似三等分線である。
この三等分の誤差は角60度に対し約2分。
********** Karajordanoff_desc.dwg ***********
この図面とアニメーションの作成方法:
プログラム Karajordanoff.lsp を (load "Karajordanoff") でロードする。
次にコマンド ラインから Karajordanoff と実行命令をタイプする。
この近似法は1919年に Kopf が発表し、その後 ドイツの数学者 Oskar Perron(1880-1975)
と フランスの数学者 Philbert Maurice d'Ocagne(1862-1938) により改良が加えられた。
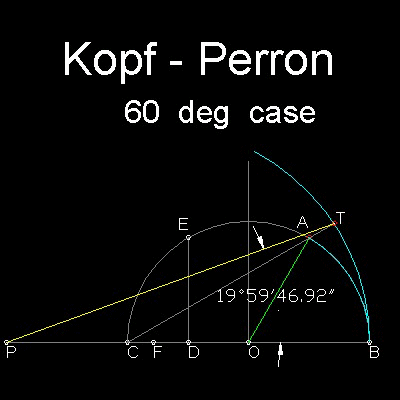
∠AOB を三等分する角とする。
点 A,B, C は単位円上。D はOC の中点とし、ED はOC に垂直とする。
点F と点D との距離DF はED の1/3 の長さとし、CP = CO= 1 とする。
点F を中心に半径がFB となるような弧を描く。
線CA の延長線は点T で弧と交差する。
線分TP は近似三等分線である。
この三等分の誤差は角60度に対し約13秒である。
*********** Kopf-Perron_desc.dwg ************
この図面の作成方法:
プログラム Kopf_Perron.lsp を (load "Kopf_Perron") でロードする。
次にコマンド ラインから Kopf_Perron と実行命令をタイプする。
小さな角に対して驚くほどの精度を持つこの非常に簡単な方法は、d'Ocagne が1934年に発表した。
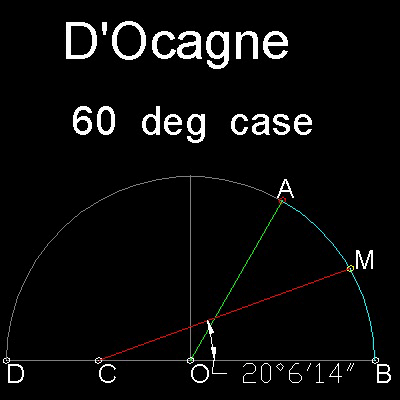
∠AOB を三等分する角とする。
点A と点B は単位円上。
点C は単位半径の中点とする。
点M を弦AB の中点とする。
線分CM は∠AOB の近似三等分線である。
この例では∠AOB = 60度に対し、誤差は僅か6'14"(6分14秒)で
非常に良い近似である。
************ D'Ocagne_desc.dwg *************
この図面の作成方法:
プログラム D'Ocagne.lsp を (load "D'Ocagne") でロードする。
次にコマンド ラインから Docagne と実行命令をタイプする。
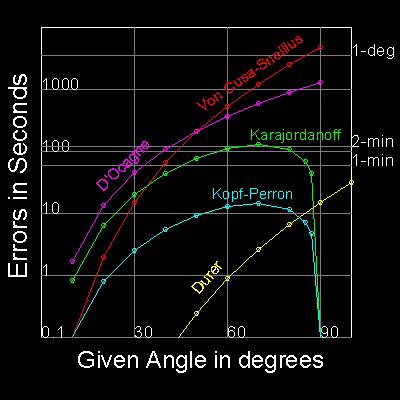
5つの近似法の誤差をグラフに示す。
誤差の値(秒)は0.01 以下から5000 の範囲をとるため、Y軸はLog対数表示にする。
表示の関係上、値0.1 以下は全て0.1 とした。
************ compare_errors.dwg *************
この図面の作成方法:
プログラム compare_errors.lsp を (load "compare_errors") でロードする。
次にコマンド ラインから compare_errors と実行命令をタイプする。
1. Yates,Robert Carl : "The Trisection problem" , pp.47-56
質問、問い合わせは 筆者 岩本 卓也宛てにお願いします。
Last Updated Nov 22, 2006
Copyright 2006 Takaya Iwamoto All rights reserved.