折り紙

ホームページの内容目次に戻る角の三等分

折り紙による三等分

折り紙の方法を用いると一枚の正方形の紙だけで角の三等分ができる。
この方法は阿部恒が発明し日本の学会誌「数学セミナー」（1980年版）に発表した。

三等分の仕方

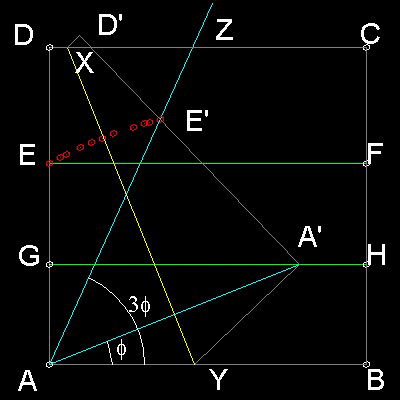
1. 三等分する角をZABとする。辺ADを
右へ移動し、折り線AZをつける。

2. 辺DC をAB と平行になるように
移動し、折り線EF をつける。

3. 辺AB がEF と重なるようにして
折り曲げ、折り線GH をつける。
GH は ABEF の二等分線となる。

4. 点A の隅を掴み、点E が線AZ と
重なるまで点A を線GH に沿って移動
させたら折り線YX をつける。

5. 移動したA とE の最終位置は
A', E'で示す。
線分AA' は∠ZAB を三等分する。

ここをクリックしてアニメーションを見る。
******** origami_tri_desc.dwg ********

この図面とアニメーションの作成方法：
   プログラム Abe_H.lsp を   (load "Abe_H") 　でロードする。
  次にコマンドラインから Abe_hisashi 　と実行命令をタイプする。
  この動作を見るには abe_h1 & abe_h2 　と実行命令をタイプする。

代表的な３つのビューポートを示す：

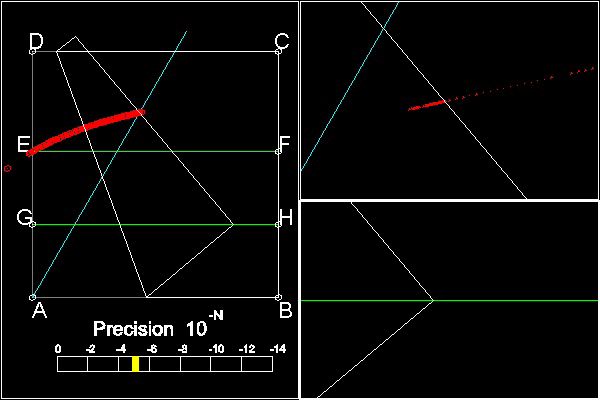
左のビューポート：
精度バーを示した全体図

右上のビューポート：
赤い点は、E' の位置を表す。
水色の線にまでくるようにする。

右下のビューポート：
点A' は緑の線GH に沿って移動する。
この時カーソルはこのビユーポートに位置しておく。

プログラムの実行は、点E' を水色の線に近づけ、
右下のビューポートで点A' を移動させると終了する。
点E' から水色の線に垂直に下ろした距離は
左のビューポートの精度表示板に示される。
この例では、距離が10の-5乗( = 10^-5 )
の場面を示している。
******** Abe_Hisashi_60_deg.dwg ********

実行例：角度が60度の場合

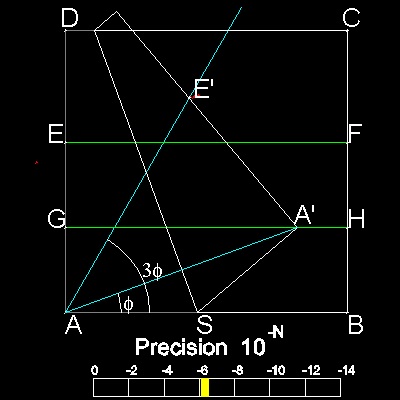
******** origami_60_deg_case.dwg ********

他の２つの方法との比較

阿部恒の方法を石斧(tomahawk)と大工用直角定規(carpenter's_square)と比較すると、
幾何学的には全て同じ原理に基ずくものであることが解かる。
参考のため　これら３つの方法を三等分角が60度の場合で実行したときの結果を
全て同じ位置関係と同じ尺度で表示してみよう。

******** compare_three_methods.dwg ********

この図面とアニメーションの作成方法：
プログラム Abe_H.lsp を (load "Abe_H") 　でロードする。
次にコマンドラインから three_methods 　と実行命令をタイプする。
このプログラムを実行するには下記の図面ファイルが必要。
******** comparison_carpenter's_square.dwg ********
******** comparison_tomahawk_bare.dwg ********
******** comparison_origami_bare.dwg ********

点P を求める解析曲線(Analytical Curve)

この章の最初の図面を見ると、点E と点P を通る曲線があることに気が付く。
筆者は、距離BH を使って、その距離をパラメータ m で表し、式を導いた。
結果は次の通り：

(x/m)² = {(1 + y/m) (y/m - 2)²} / (3 - y/m)

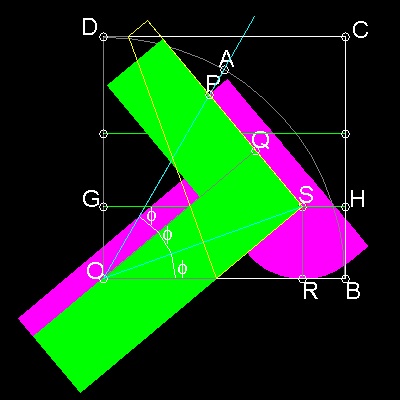
ここでは、座標の原点をO 、OB をX軸, OD をY軸とする。

******** origami_curve.dwg ********


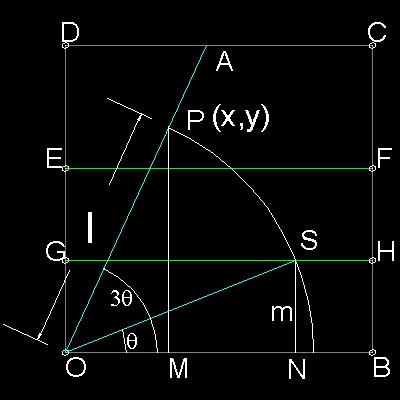
 図面の中では OP = OS = l および ∠SON = (1/3)∠PON　とする。
 三角形SON においては、
	l*sin(θ) = m　のとき、l = m /sin(θ)　である。
 三角形POM においては、
	x = l*cos(3θ) = m*cos(3θ)/sin(θ) となる------(1)
 更に y = l*sin(3θ) = m*sin(3θ)/sin(θ)
      = m*(3sin(θ) - 4sin³(θ))/sin(θ)
      =(3 - 4sin²(θ)*m = (4cos²(θ) - 1)*m
 であるから、
	4cos²(θ) - 1 = y/m,
  または  cos²(θ) = (1/4)(1+y/m) ------(2)
　　となる
(1)から、x²sin²(θ) = m²cos²(θ)cos²(3θ)
	= m²cos²(θ)(4cos²(θ) - 3)² -------(3)
　が導かれる。
 ここで、 cos²(θ)  と (y/m)　の関係 (2) を用いると
	 sin²(θ) = 1 - cos²(θ) = (1/4)(3 - y/m)
	 cos²(θ) = (1/4)(1 + y/m)
	 4cos²(θ) - 3 = y/m - 2
 であるから,これを(3)に代入すると
 
	x² = m²{(1 + y/m) (y/m - 2)²} / (3 - y/m)　
 
　となる。これが折り紙による三等分曲線(Origami Trisectrix)である。
　さらに　X = x/m, Y = y/m とおいて無次元化すると
	X² = {(1 + Y) (Y - 2)²} / (3 - Y)
 または　
	X²(3 - Y) = (1 + Y) (Y - 2)²
　とも表される。

折り紙曲線を用いた三等分の例

この曲線を用いた角の三等分の例を示す。

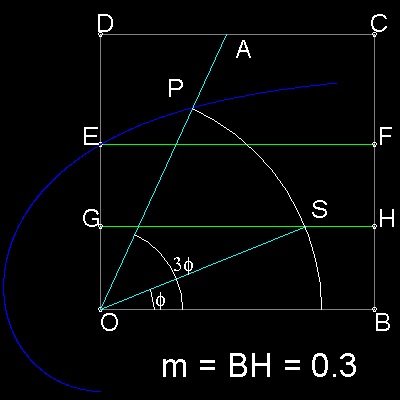
ステップ (1): 三等分する角を示す点A を指定する。

ステップ (2): m=0.3（任意で良いが、BH の長さに等しい値）
の折り紙曲線を描く。

ステップ (3): OA とこの曲線の交点をP とする。

ステップ (4): 中心がO で、半径OP の円を描く。

ステップ (5): この円が線分GH を切断する点をS とする。

ステップ (6): 線分OS は∠AOB を三等分する。
******** origami_curve_trisection.dwg ********

この図面とアニメーションの作成方法：
プログラム Abet.lsp を (load "Abet") 　でロードする。
次にコマンドラインから type Abe_4 　と実行命令をタイプする。

参考文献

1. 阿部　恒:"すごいぞ折り紙" 日本評論社 , 2003. ISBN4-535-78409-4
Hisashi Abe: Published in Japanese--Amazon.com link