追跡曲線の話題

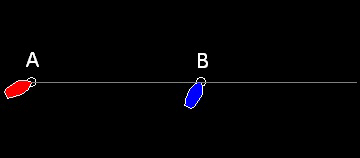
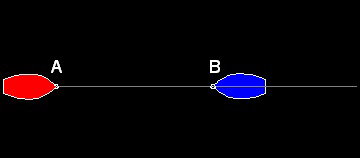
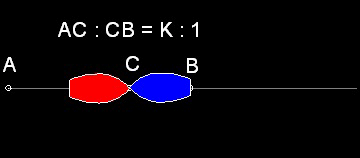
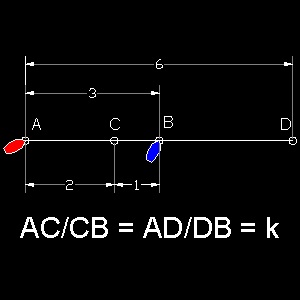
ボートの追いつき方--Apollonius circle このページに掲載するアニメーション（アニメーションを見るにはテキストをクリックして下さい。） (a) 互いに向き合っている場合 (b) 同じ線上を追いかける場合 (c) より一般的な場合 問題 一番目の船(青色で示す)が点B を出発し一定のスピードである方向に進んでいる。霧のため視界が悪くほかの船が 追いかけていることに気が付かないのでずっと同じ方向に進むと仮定する。 二番目の船(赤色で示す)は点A を同時に出発し、一番目の船のK倍のスピードで進む。海面は平面であると仮定する. 二番目の速い船が遅い船をできるだけ短い時間で追いつくにはどのコースを進めば良いか？ ******* Apollo_circle_00.dwg ******** 両方の船が同じ線上にある場合の簡単な二つの仮定から始める。 (a)  互いに向き合っている場合 ２隻の船が点C で出会うことは容易に予想できる。その場所は、線分AB 内を K:1 の比で分割した点、即ち AC:CB = K : 1　である。 ******* Apollo_circle_01.dwg ******** ******* Apollo_circle_01A.dwg ******* ここをクリックしてアニメーションを見る。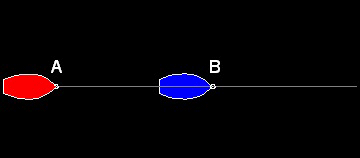 (b)  同じ線上を追いかける場合 この場合の追跡者は、点D で遅い船に追いつく。それは線分AB の延長線をK:1 の比で分割する点、即ち AD:BD = K:1　である。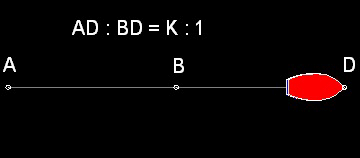 ************* Apollo_circle_02.dwg *************  ************ Apollo_circle_02A.dwg ************* ここをクリックしてアニメーションを見る。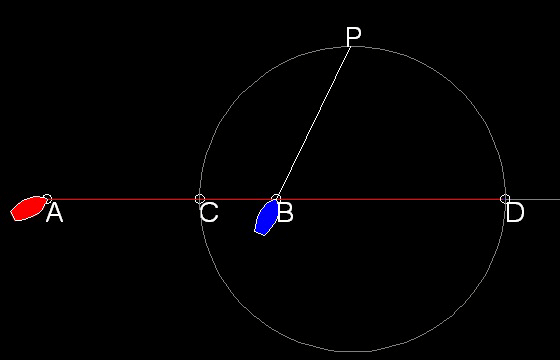 (c)  一般的な場合 下図に示すように　遅いボートが　線分AB とは同一線上でない方向へ動いている場合、 ボート "A" はどの方向に進むべきか？ ********* Apollo_circle_00.dwg **********  ************** Apollonius_circle_1.dwg ***************    プログラム pursuit_Apollonius.lsp を   (load "pursuit_Apollonius")　でロードする。    コマンド ラインから    pursuit_test_3 　と実行命令をタイプする。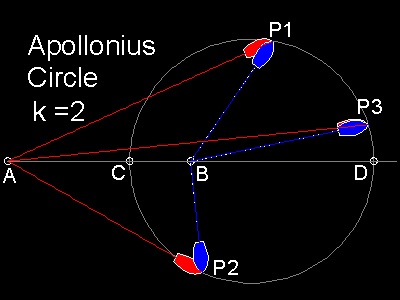 青い船の進む方向を色々変えて　赤い船が何処で追いつくかを試してみた結果が上の右図である。 速度が一定ならば　どんな方向に進んでも　必ず　CDを直径とする円周上で追いつくことがわかる。 何故そうなるのかを　調べてみよう。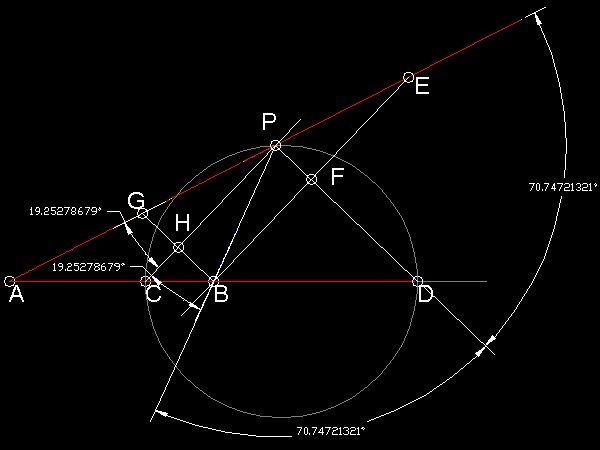 追いつく点をP とすると、点P は次の条件を満たす： AP:BP = K : 1 例えば、K の値を2 に設定。 中心をB とし半径をR1 とする円を描く。次に中心をA とし半径がR1 のK 倍の円を描く。 交点を求める。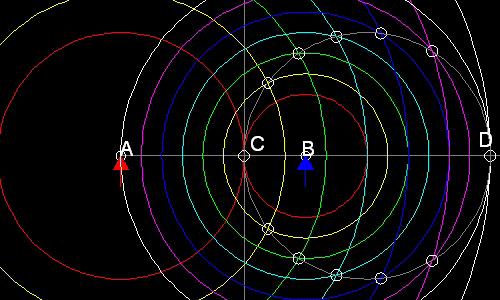これを数回繰り返すと、結果は次の通り： ************************ Apollo_03.dwg ************************** この結果から次のことが判る： 1. 点C と D は一対の円が接する時の場合である。（赤色と白色の円） 2. 全ての交点は直径をCD とする円上にある。（黄色、水色、青色、紫色の円） 複数のアポロニウスの円を描くためには    プログラム pursuit_Apollonius.lsp を   (load "pursuit_Apollonius")　でロードする。   コマンド ラインから    test_circle 　と実行命令をタイプする。 このプログラムは　 red_arrow.dwg と blue_arrow.dwg が必要です。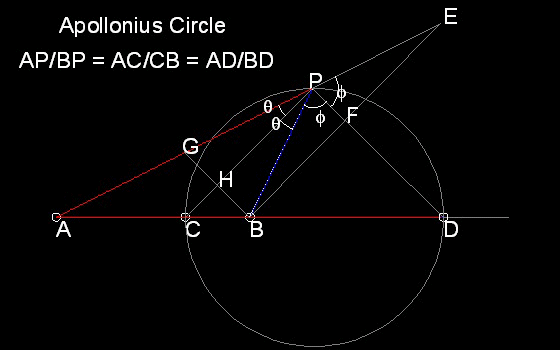 ギリシャの数学者アポロニウス(Apollonius)は、 円は "全ての点が一点から等距離にある" という一般定義とは 全く異なる方法で定義できることを発見した。 アポロニウスによるその定義は次のように言い表わせられる。 ある固定点からの距離が,もう一つの固定点からの距離の定数倍であるように移動する点の軌跡は円である。 遅いボートに追いつくために追跡者が何をすべきかは明らかである。 K の値に基づいて、C と D の位置を求める。 CD を直径とする円を描く。 遅いボートが向かっている円上の点P を求める。 点P 方向へボートの舵をとる。 ここをクリックしてアニメーションを見る。 この図面とアニメーションの作成方法：    プログラム pursuit_Apollonius.lsp を   (load "pursuit_Apollonius")　でロードする。 (a),(b),(c)の場合を見るには    コマンド ラインから    pursuit_test 　と実行命令をタイプする。       (a), (b), (c) の場合が続けて実行される。 注*： このプログラムは red_boat.dwg と blue_boat.dwg が必要です。 ********************** Apollo_1c_0.dwg ************************

一般的な場合を実行したら結果はこのようになる。

点C と D は何が特別なのか？

∠APC, ∠CPB, ∠BPD, ∠DPE を計ると、点C とD は三角形APB の頂点P での内角と外角の両方の角をそれぞれ二等分することが判る。

きちんとした証明はこのページの後方で行う。




******************* pursuit_Apollonius_01.dwg ********************

 更にアポロニウスの円について：
 A と B の中点をO とし、AO = BO = r　とすると
	OC = r*(K-1)/(K+1)	
	OD = r*(K+1)/(K-1)
 アポロニウスの円の直径は        r * 4K/(K2 -1)　
 中点"O"から円の中心までの距離は r*(K2 + 1)/(K2 - 1)　

幾何学証明について

上記の説明はApollonius が証明した次の定理に基づいている。

1. AB が C と D で調和的に分割されると、CD も A と B で調和的に分割される。

   CB/BD = AC/AD

2. 三角形における角の二等分線は、向かい側の辺を隣接する辺の長さの比に分割する。

   AC/CB = AD/BD = AP/BP = K

次の図では、 CP と DP は角の二等分線で、

CP は BE に平行、BG は DP に平行である。

証明のまとめ：

三角形ADP において、BG は DP と平行であるから、AD/BD = AP/GP = AP/BP　である。

この図面とアニメーションの作成方法：
   プログラム pursuit_Apollonius.lsp を   (load "pursuit_Apollonius")　でロードする。
(a),(b),(c)の場合を見るには
   コマンド ラインから    pursuit_test 　と実行命令をタイプする。
      (a), (b), (c) の場合が続けて実行される。
注*： このプログラムは red_boat.dwg と blue_boat.dwg が必要です。
************************ Apollo_circle_03.dwg ***************************

参考文献 Ogilvy,C.S. : Excursions in Geometry. Dover, p. 13,1990. Originally published by Oxford in 1969. Ogilvy,C.S. : Excursions in Mathematics. Dover, p. 83 & 148,1994. Originally published by Oxford in 1956. Steinhaus,H.: Mathematical Snapshots. Dover, p. 111, 1999. Originally published by Oxford in 1983.

質問、問い合わせは　筆者 岩本　卓也　宛てにお願いします。

Last Updated Aug-10th, 2006

Copyright 2006 Takaya Iwamoto   All rights reserved.