三角形の頂点にいる犬がそれぞれの隣の犬の尻尾を追いかける--ブロカール点(Brocard Point)、等角螺旋
このページにあるアニメーションのリスト(ハイパーテキストをクリックするとアニメーションがみられます。)
ここにもどるにはブラウザーの"Back" ボタンを使う。
| ブロカール点の定義 ブロカール点の定義 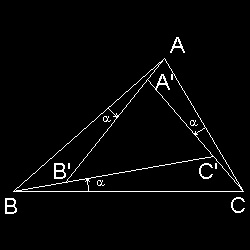 |
3匹の犬追跡 - 時計回り 時計回り追跡 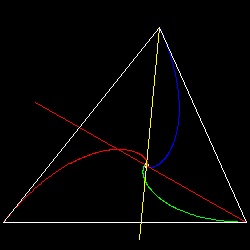 |
3匹の犬追跡 - 反時計回り 反時計回り追跡 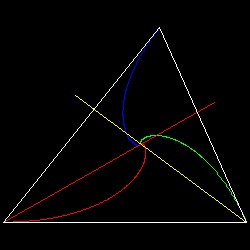 |
三角形が正三角形ならば、3匹全ての犬は同じスピードで三角形の中心に集まってくる。
しかし正三角形でなかったら、果たして 犬は一点に集まるのだろうか?
答えは、YES ! 集まります。もちろん犬の速度は皆同じではありませんが。
前の章からの引用で、3匹の犬が一点に集まる条件は、
これを達成できる方法例を下図に示す。
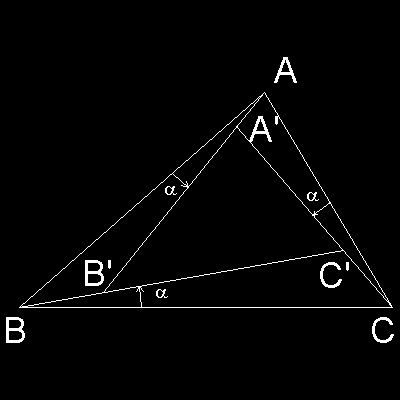
左図から
∠ ABC = ∠ ABC' + α = ∠A'B'C'
∠ BCA = ∠ BCA' + α = ∠B'C'A'
∠ CAB = ∠ CAB' + α = ∠C'A'B'
であることが容易にわかる。
従って、∠α の値がゼロから図中に指定した方向へ増加すれば、
ΔA'B'C'は,常に元のΔABC と相似である。
∠α を 0 から180度に増加させ、わかりやすいように
BC', CA', AB' を異なる色の線にして、
A'B'C'による三角形を描くとどうなるであろうか?
その結果を下側の図に示す。
*********** Brocard_point_1.dwg ************
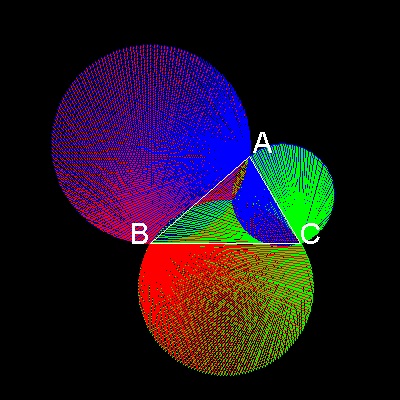
**************** Brocard_defa.dwg ****************** ************** Brocard_defa_zoom.dwg ***************
この図面とアニメーションの作成方法:
プログラム brocard.lsp を (load "brocard") でロードする。
次にコマンド ラインから brocard_defa と実行命令をタイプする。
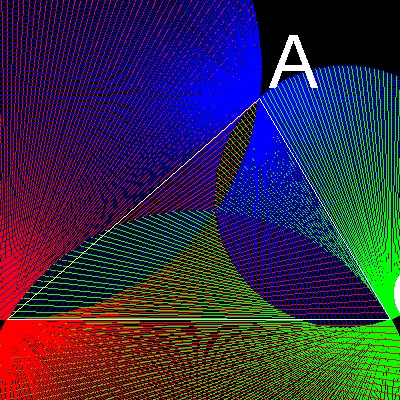
ここで2つの事実を容易に気付くことができる。
(1) 三角形がゼロに収束する点が三角形の中心付近にあること。
(2) この点は3つの円の交点であること。
一番目の円は点A を通り、線分BC と点B で接する。
二番目の円は点B を通り、線分CA と点C で接する。
三番目の円は点C を通り、線分CA と点A で接する。
**右側の拡大図は、このような点を図によって定義する一つの方法でもあることに注目。
犬が集まる点は、
1875年にフランス軍人のアンリ ブロカール(Henri Brocard)
(1845-1922)
が論文を発表して以来、
ブロカール点 (Brocard Point) と呼ばれるようになった。しかしブロカール以前の1816年に既に
Carl Jacobi(1804-1851) と
August Crelle(1780-1855)
によってこの問題は解かれている。クレル(Crelle)はこの特性の発見に驚いて次のように書き残している。
"こんなに単純な三角形にこのような奥の深い特性が潜んでいることは本当に驚きである。 この他の形状にも未だ知られていない特性が
どれほどの数あるのであろうか ?"
クレルは19世紀後半の幾何学ルネサンスを見事に予想していたことになる。
ただ、二人がやった事はブロカールが数学家達の関心を
再復活させるまで忘れられてしまっていた。
1875年頃から約半世紀位の間、ユークリッド幾何学 (Euclidean Geometry) が再び多くの数学者達から注目を浴び、
多数の素晴らしい成果が論文に発表された。ブロカール点 (Brocard point)はその中でも人気のあるテーマであった。[8]
今ではその位置を求める方法は幾つもあることが判っている。
3匹の犬の追跡は、位置が決まれば、この点と各犬の最初の位置との距離に比例した犬の速度をそれぞれに設定して始められる。
一般にはブロカール点は2つある。これらは3匹の犬の追跡における時計回りと反時計回りの場合の到達地点である。
その二つの場合を下図に示す。
反時計回りの追跡(点 A -> B ->C)は点 "P" で終わり、 時計周りの追跡(点 A -> C -> B)は点 "Q" で終わる。
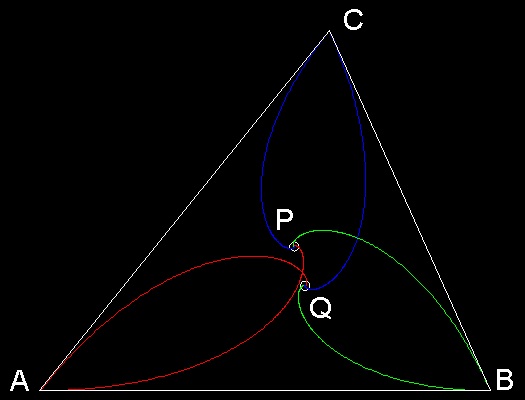
****************** Brocard_pnt_1.dwg *******************
この図面の作成方法:
プログラム brocard.lsp を (load "brocard") でロードする。
時計周りの追跡 (Q)
コマンド ラインから brocard2_cw と実行命令をタイプする。
実行を終了したら (single_win) と実行命令をタイプする。
次に "Extent" オプションでズーム拡大する
反時計周りの追跡 (P)
コマンド ラインから brocard2_ccw と実行命令をタイプする。
実行を終了したら (single_win) と実行命令をタイプする。
次に "Extent" オプションでズーム拡大する
注: 犬が取る単位ステップ(=スピード)の長さは、点A,B,C からブロカール点 (P & Q)までの最初の距離に比例する。
注*:このプログラムは prec_bar.dwg と prec_meter.dwg が必要です。
ブロカール点の求め方
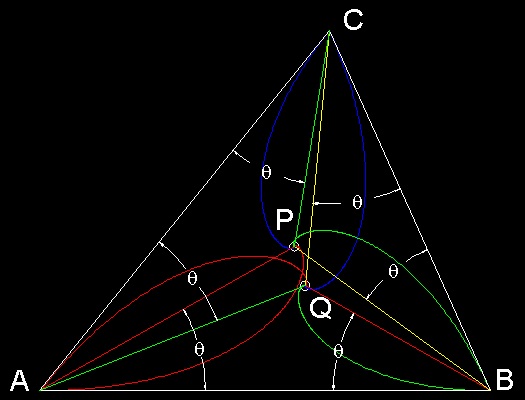
どんな三角形おいても、点P,Q で示すようなブロカール点 が存在し それを定義する ユニークな角 θ を
ブロカール角 (Brocard Angle) と呼んでいる。
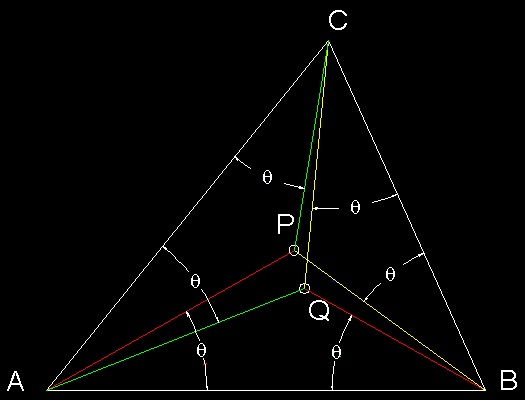
****************** Brocard_pnt_2.dwg *******************
前の章で述べたように、追跡曲線の円弧の長さは各頂点から中心(点P と Q)の距離に比例する。
例えば反時計回りの場合、初め点Aにいた犬が点Bにいた犬に追いつくまでに移動する円弧の長さはAP/cos(θ)である。
点A,B,Cでの3匹の速度が、距離AP, BP, CPに比例して設定されると、これらの3匹の犬は点P
で出会う。
時計回りの追跡の場合は点Pを 点Qで置き換えて考えればよい。
******************* Brocard_pnt_3.dwg ********************
前の章で示した正三角形の場合は、P と Q が同じ位置にある特別な場合である。しかし一般三角形の場合では、
時計回りと反時計回りの2つのブロカール点ができる。
解析的ブロカール点の定義:
ブロカール角 (Brocard angle) は次の方程式で与えられる: cot θ = cot A + cot B + cot C (∠A, ∠B, ∠C はそれぞれ点 A,B,C の角)幾何学的ブロカール点の定義:
ブロカール点は、次の図に示すようにひとつの頂点を通り、隣接する頂点で向かいの辺に接するような円の交点として幾何学的に求められる。
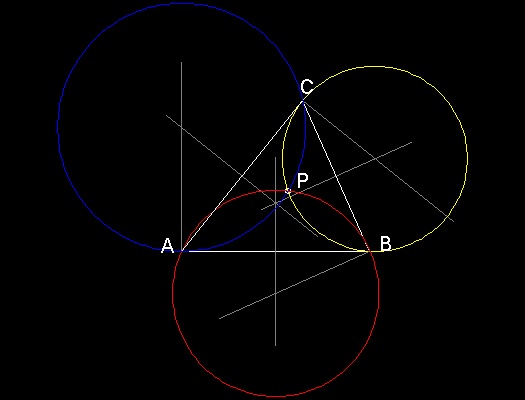
反時計周りの場合:
Cを通り 点A でABに接する円
Aを通り 点B でBCに接する円
Bを通り 点C でCAに接する円
**************** Brocard_ccw_geom.dwg ****************
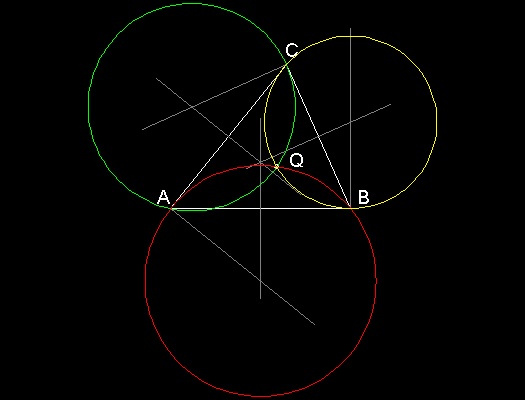
時計周りの場合:
Aを通り 点C でBCに接する円
Cを通り 点B でABに接する円
Bを通り 点A でCAに接する円
**************** Brocard_cw_geom.dwg *****************
ブロカール点(続き)
ブロカール点を幾何学的に求めるには(つまり3つの円が交わる点)、copy_rotate 関数を使ってこれらの円の中心を求めると簡単である。
点A とB を結ぶ線分の垂直二等分に関しては、線分ab を選択し回転の中心とする中点を選択、そして90度回転させる。
(この場合プラス/マイナスは関係ない)
点A で線分ACに垂直な線分を引くには、この copy_rotate コマンドを実行し、線分AC を選択、点A
の回りに -90度回転させる。
(この場合はマイナスが時計回り) これら二つの線分による交点は円の中心で、ブロカール点を定義するのに用られる。
ブロカール点を求めるもう一つの方法は[8]に述べてある。
その方法は:
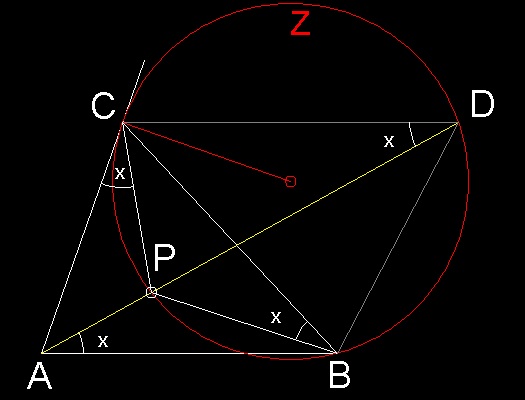
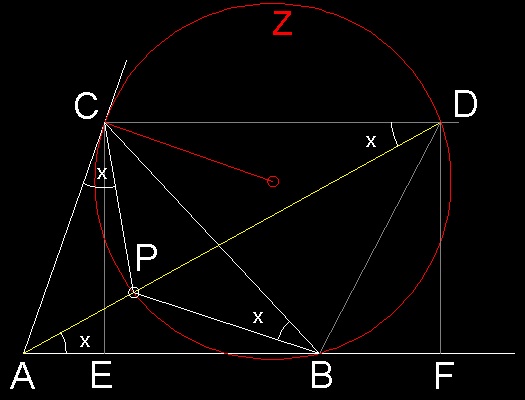
点B を通り点C で線分CA と接する円 (Z) を描く。
点C を通りAB に平行な線分が点D でZ と交わるならば、DA はブロカール点 P でZ と交差する。
****************** Brocard_angle_0.dwg ******************
∠ CDP= x と置くと
∠ PCA = ∠ PAB = ∠ PBC = x
その理由は:
- ∠ PCA (CA は接線で CP は弦であるため)
- ∠ PAB (CD // AB であるため)
- ∠ PBC は ∠ CDP と同じ Z の一部 (CP を共有)
****************** Brocard_angle_1.dwg *****************
ここで、DF はAB に垂直、CE はC からABにおろした垂線である。
CEFD は長方形で CE = DF である。CA はZ への接線であるから、
∠C = ∠ ACB = ∠ CDB で、更にCD と AF は平行であるから
D とB における錯角は等しくなる。 つまり ∠ DBF = ∠ C となる。
∠ DAF = x とおき DF = CE である ことを 使うと
cot(x) = AF/DF = (AE + EB + BF)/DF = AE/CE + EB/CE + BF/DF
ここで AE/CE = cot A , EB/CE = cot B , BF/DF = cot C
であるから ブロカール角 が次のような式で求まることがわかる。
一般的な三角形の場合の結果例
-反時計回りの追跡-
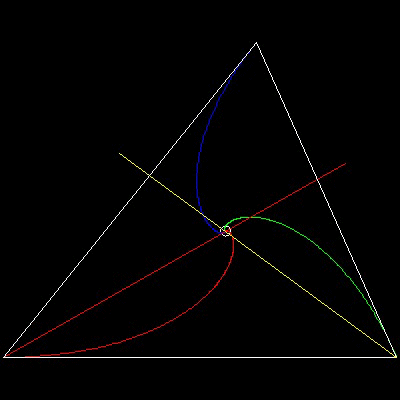
この図面とアニメーションの作成方法:
プログラム brocard.lsp を (load "brocard") でロードする。
コマンド ラインから brocard2_ccw と実行命令をタイプする。
(setup_tri_ccw) はブロカール点を持つ三角形ABC を設定する。
(c:omega) は次の方程式を用いてブロカール角 "omega" を計算する cot q = cot A + cot B + cot C (∠ A, ∠ B, ∠ C は点 A,B,C におけるそれぞれの角度)********** 3dogs_ccw_result.dwg *********
-時計回りの追跡-
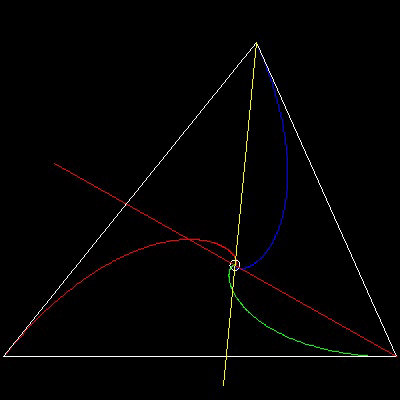 この図面とアニメーションの作成方法:
この図面とアニメーションの作成方法:
プログラム brocard.lsp を (load "brocard") でロードする。
コマンド ラインから brocard2_cw と実行命令をタイプする。
(setup_tri_cw) はブロカール点を持つ三角形ABC を設定する。
(c:omega) は三角方程式を用いてブロカール角 "omega" を計算する cot θ = cot A + cot B + cot C (∠ A, ∠ B, ∠ C は点 A,B,C におけるそれぞれの角度)********** 3dogs_cw_result.dwg **********
次は自分で試してみて下さい。
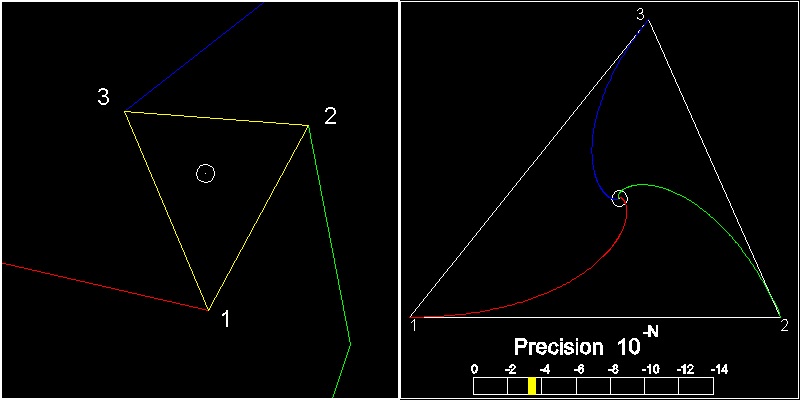
************************************* ccw_result_1.dwg
*************************************
3つの端点をつなぐと三角形ができます。頂点の番号の付け方の方向ははじめの三角形の頂点の方向に応じて決まります。
赤色の端は"1", 緑色の端は"2", 青色は"3" という具合です。
黄色い三角形の点2 と 3 をはじめの三角形の点2 と 3 に一致させてみると、両方の三角形は相似になっています。
(同じ角で尺度が違うだけ!!)
それを確かめるには CAD のコマンド の "ALIGN" をつかって小さいほうの三角形を 大きいほうに "ALIGN" させてみると
わかります。
または 角度を測って比べてみてもよい。
このことは正方形の中庭での4匹の犬の場合にも当てはまることです。つまり 4匹の犬の位置関係は追跡している間ずっと
正方形(最初の形と相似な形状) を保っていたことを想い起こしてください。
その他のおもしろいブロカール点の特性
ブロカール点については、おもしろい特性がたくさん見つかっている。さらに勉強したい方は、ブロカール点とそれに関するテーマについて書かれた素晴らしい本[8]を参照されることをお勧めする。
ホームページの内容目次に戻る 追跡曲線について
質問、問い合わせは 筆者 岩本 卓也 宛てにお願いします。
Last Updated Oct 9-th, 2006
Copyright 2006 Takaya Iwamoto All rights reserved.