ギリシャの数学者達による立方体の倍積

ニコメデス(Nicomedes)のコンコイド

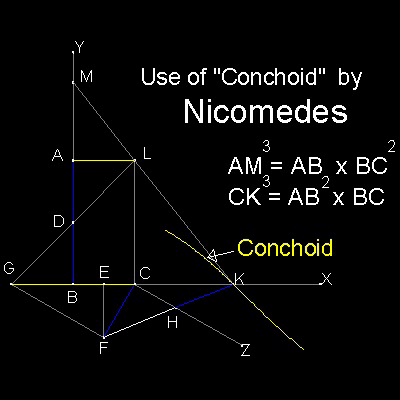
ニコメデス(Nicomedes)は、デリアン問題を解くためにコンコイド(Conchoid)と呼ばれる曲線を発明した。
これは、線分FK が線分CZ 上の点H を通り、HK = CF を満たしながら x-軸を切断するようなX-軸上の点K を求めるのに用いられる。

この方法は、角の三等分法でのアルキメデスやパップス、その他多くのギリシャの数学者が用いた"Verging"(neusis)と似ている。

コンコイドを用いた解

 
 四角形ABCLを作る。 D と E は AB と BC の中点。

 x-軸上に G を作るように LD を伸ばす。x-軸に EF を垂直に伸ばし CF = AD とする。
 CZ をGF に平行に描く。 HK = CF となる x-軸上の点K を選択する。 
 このような点が特殊曲線コンコイド("conchoid")とx-軸との交点。 
 この曲線は F が棒"pole"で、CZ が目盛り"rule"、CF が距離"distance"の時に描かれる。 
 別のやり方では、辺上に長さ CF を印した定規を使い、FK の位置を見つける(verging,or neusis process)。

 点K が見つかったら、線分KL を延長してy-軸上の点M を作る。

 その時　AM = {AB.BC2}1/3 で CK = {AB2.BC}1/3　となる。

コンコイド("conchoid")を使った方法を見るにはここをクリックしてアニメーションを見る。
******** Nicomedes_Delian_desc.dwg *******

この図面とアニメーションの作成方法： 
  プログラム Nicomedes_Delian.lsp  を (load "Nicomedes_Delian") でロードする。
  次にコマンドラインから test_0 と実行命令をタイプする。

neusis(verging)を使った解

この図面とアニメーションの作成方法： 
  プログラム Nicomedes_Delian.lsp  を (load "Nicomedes_Delian") でロードする。 
  次にコマンドラインから Nicomedes_Delian と実行命令をタイプする。

AM と CK が解であることの証明

ヒース(Heath)の証明： 最初のステップでは　MD = FK　を見せる。 E は BC を二分することから、 BK.KC + CE2 = KF2 である。 (注記： (a + b) (a - b) = a2 + b2 ) EF2 を両側に追加 BK.KC + CF2 = KF2 (1) AL は GK　に平行であるから、 CL も MB　に平行。 MA / AB = ML / LK = BC / CK しかし AB = 2 AD　で　 BC = (1/2)GC　である。 故に MA / AD = GC /CK = FH / HK　そして MD / DA = FK / HK ここで　DA = HK　である、従って MD = FK　となる。 D は ABを二分するため、 MD2 = BM.MA + DA2 MD = FK　であるから(1)と合わせると BM.MA + DA2 = BK.KC + CF2 しかし DA = CF;　よって BM.MA = BK.KC そして CK/MA = BM/BK = LC/CK, ところが三角形では MAl と MBK, BM/BK = MA/AL 従って LC/CK = CK/MA = MA/AL 　または AB/CK = CK/MA = MA/BC それ故 AM = {AB.BC2}1/3 および CK = {AB2.BC}1/3

質問、問い合わせは 筆者 岩本 卓也宛てにお願いします。

Last Updated Nov 22, 2006

Copyright 2006 Takaya Iwamoto   All rights reserved.