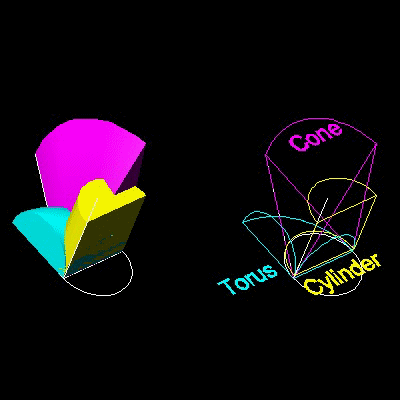
アルキタス( Archytas of Tarentum, およそ 428 BC-350 BC)
は三つの回転面の交差を求める解を発見した。
使用する三つの回転面は
(1) 直円錐: x2 + y2 + z2 = (a/b)2x2
(2) 円柱: x2 + y2 = a x
(3) 円環:
x2 + y2 + z2 = a {x2 + y2}1/2
但し AC = a および AB = b とする。
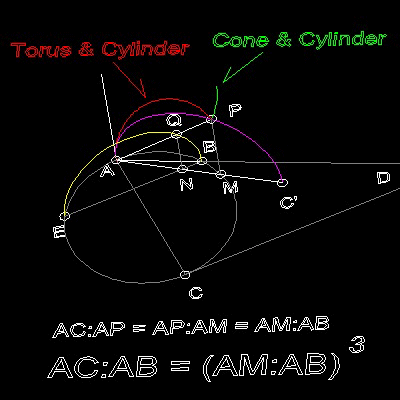
図から、AC/AP = AP/AM = AM/AB を求まる。
よって AC/AB = (AM/AB)3 で、AM が解である。
詳しくは アルキタス(Archytas)- 3D 立体相接解 の章で説明。
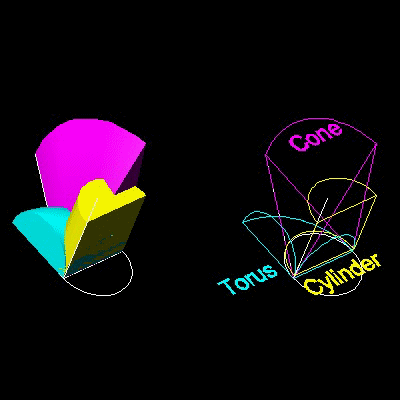
********* Archytas_Delian_model.dwg
********* ******** Archytas_Delian_result.dwg
********
エウドクソス( Eudoxus of Cnidus, 408 BC - 355 BC) はアルキタス( Archytas)の生徒であった。彼は円錐と円環の相接を
xy平面上に射影することによって問題を解いた。その解は、曲線が円ABCと交差する点にある。
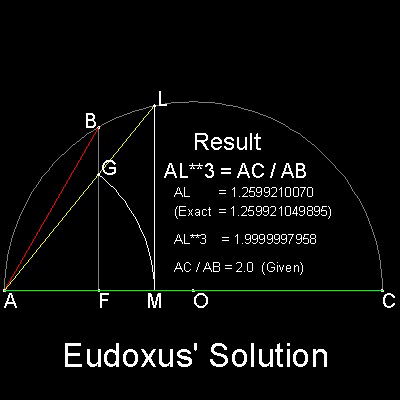
AB と AC は線分で、この線分間で二つの比例中項を見つける。
ステップ:
1. 線分ACに垂直な線BF を引く。
2. BF 上に任意の点G をとり、A を中心とし半径AG の弧を描き、
線分AC との交点を M とする。
3. 点M でAC に垂直な線を引く。この線は点L で線分AG に交差する。
4. 点L が円周上に来る時のAL が解である。
ここをクリックしてアニメーションを見る。
********** Eudoxus_Delian_desc.dwg
*********
詳しくは エウドクソス(Eudoxus)のデリアン問題 の章で説明。
メナケムス( Menaechmus, およそ 380 BC - 320 BC),
は円錐曲線を発見した人であると言われ、アレクサンダー大王に
”幾何学に王道なし”と答えたことで有名。 彼はデリアン問題を解くのに放物線と直角双曲線を用いた。
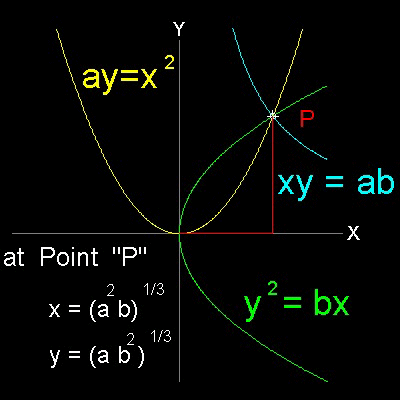
x, y を線分a, b 間の二つの比例中項が
a / x = x / y = y / b
であるとすると x2 = ay, y2 = bx
および xy = ab である。 よって、これらの3曲線のいずれの組合わせでも デリアン問題の解を与える。 |
[アニメーションをここに追加]
******** Menaechmus_Delian_desc.dwg
*******
詳細は メナケムス(Menaechmus)のデリアン問題 の章で説明。
多くの歴史家は、この解がプラトー(Plato, 427 BC - 347 BC) によるものでないと認めている。
一般的な結論としては、この解は、プラトーの時代または メナケムス(Menaechmus)(およそ 380 BC - 320 BC) 以後に、
プラトーのアカデミー内部の誰かによって発明されたものだと考えられる。
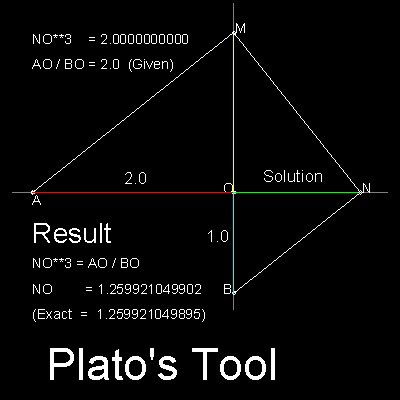
この基本概念は、∠AMN と ∠MNB が90度の角度を保ちながら、
y軸とx軸上の点M とN を求めることである。
また、3つの三角形 AOM, MON, NOB は相似である。
よって、AO / OM = OM / ON = ON / BO
および ON3 = AO.BO2
*********** Plato_Delian_desc.dwg ***********
詳細は プラトー(Plato)のデリアン問題 の章で説明。
エラトステネス(Eratosthenes of Cyrene, 276 BC - 194 BC) は地球の大きさを概算したことでも有名。
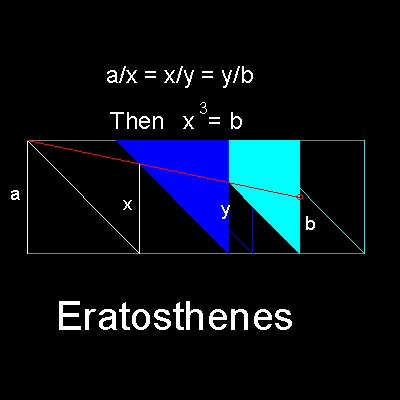
******** Eratosthenes_Delian_desc.dwg
*******
詳細は エラトステネス(Eratosthenes)のデリアン問題 の章で説明。
ニコメデス(Nicomedes , およそ 280 BC - 210 BC) はコンコイド曲線(Conchoid
curve)の発明者で、
自らの発明を使ってデリアン問題を解いた。
次に長さが等しいことを求める:
{AB.BC2}1/3 および {AB2.BC}1/3
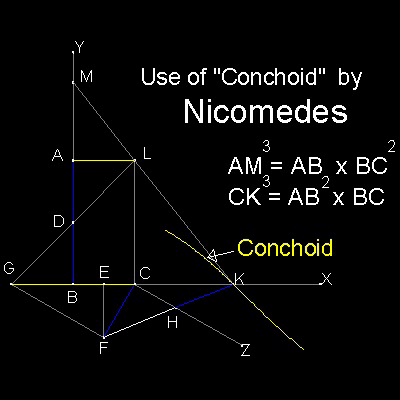
まず AB と BC の長さを与える。
D と E は AB とBC の二等分線。
CG = AB, CF = AD で、 CZ を GF に平行に引く。
CF = HK であるような点K が求まれば
AB / AM = AM / CK = CK / BC となり
AM= {AB.BC2}1/3 および CK = {AB2.BC}1/3
そのためには コンコイドは F を "ポール" に、CZ を "定規" に、
距離をCF(= AD)に等しくなるように描く。
ここをクリックしてアニメーションを見る。
********* Nicomedes_Delian_desc.dwg
********
詳細は ニコメデス(Nicomedes)のデリアン問題 の章で説明。
フィロン(Philon of Byzantine , およそ 280 BC - 220 BC) はデリアン問題を次のようにして解いた:
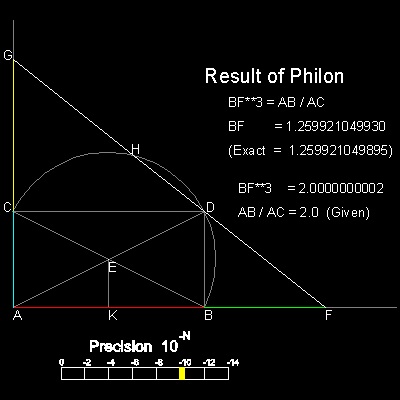
AB と AC は二つの与えられた直線。
四角形ABDC を描く。
点E は
対角線AD と BCの交点。
直径BC の半円BDC を描く。
D から線を引く。
これがF とG でAB とAC に交差する。
また、この線は半円を H で切断する。
この線分を GH = DF となるように選択した時の
BF と CG が解である。
注記)精度表示板は |GH - DF| の値を表す。
************ Philon_Delian_desc.dwg **********
詳細は フィロン(Philon)のデリアン問題 の章で説明。
アポロニウス(Apollonius of Perga , およそ 262 BC - 190 BC) の解はフィロンの解と非常に似ている。
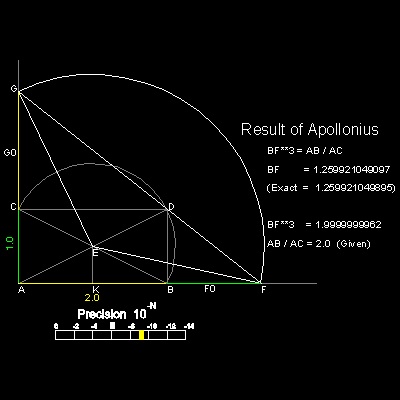
直線AB と AC、半円BDC が与えられている。
E を中心とする円が F と G で AC と AB の延長線を切断。
FD と DG を繋ぐ。
3点 F,D,G が一直線上にある時に CG と BF が解である。
********** Apollonius_Delian_desc.dwg
*********
詳細は アポロニウス(Apollonius)のデリアン問題 の章で説明。
ヘロン(Heron of Alexandria , およそ 10 AD - 75 AD)
の解はフィロンの解に非常に似ている。
違いは D を通る線分が EF = EG になるように選択されることである。
その時の CG と BF が解である。
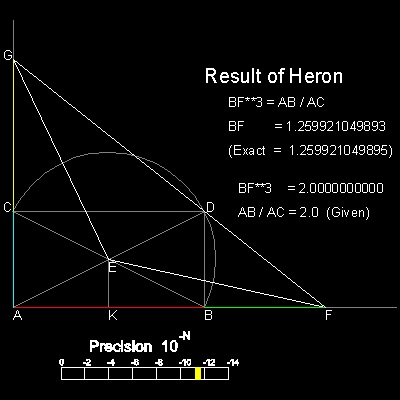
*********** Heron_Delian_desc.dwg ***********
詳細は ヘロン(Heron)のデリアン問題 の章で説明。
ディオクレス(Diocles, およそ 240 BC - 180 BC) は シッソイド疾走線(Cissoid) を発明し、その曲線をデリアン問題の解に用いた。
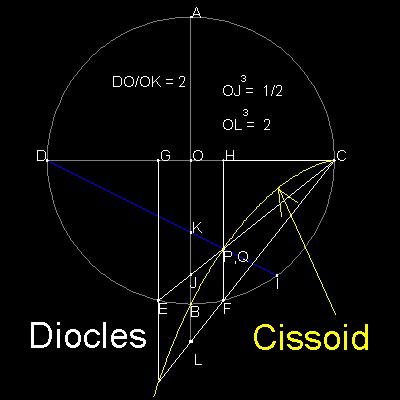
*********** Diocles_Delian_desc.dwg
**********
詳細は ディオクレス(Diocles)のデリアン問題 の章で説明。
パップス(Pappus of Alexandria , およそ 290 AD - 350 AD)
はこの本の中で、以下の方法を述べている。
名前を挙げずにある高名な数学者の考え出したものであると紹介している。
しかし 彼自身はこの方法に批判的である。
その主な理由は これが 反復法であり無限回くりかえせば 正解に近ずくことに気がつかなかったためである。
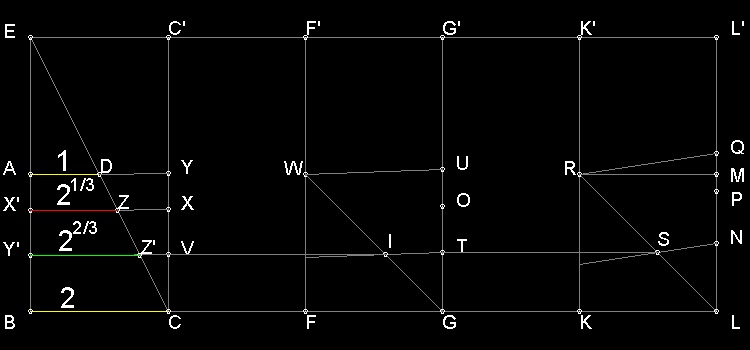
この例は 三回の反復の後の結果である。AD = 1.0, AB = BC = 2.0 から始めて
X'Z = 1.25909 (正解は(2)1/3=1.259921 )
Y'Z = 1.58643 (正解は(2)2/3=1.587401 )
*************************** approximation_Delian_desc.dwg
**************************
詳細は Approximation_Delian の章で説明。
質問、問い合わせは 筆者 岩本 卓也 宛てにお願いします。
Last Updated Nov 22, 2006
Copyright 2006 Takaya Iwamoto All rights reserved. .