ホームページの内容目次に戻る  古代ギリシャ数学の三大問題  ギリシャ時代の円の求積

ギリシャ時代の円の求積

アルキメデス(Archimedes) --「円の計測」

アルキメデス( Archimedes, 287BC - 212 BC) は、精密にpの計算を行った最初の人である。

彼の方法は、同じ円に内接する多角形と外接する多角形の周囲の長さがそれぞれ円周の下限値と上限値となるという事実に基づいている。

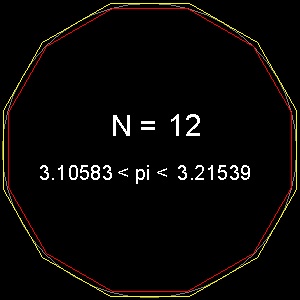
六角形と十二角形との例を下図に示す。


********* pi_hexagon.dwg ********* ********** pi_12gon.dwg *********

これらの図面では、直径を10に設定している。図面を開き周囲の長さを見て下さい。
（"LIST" コマンドか "Properties" オプションを使用）
周囲の１０分の１がp の近似値。

近代の表記法

彼のアイデアは近代の表記法では
n(2)ksin(q/2k) < p < n (2)k tan(q/2k) 　　で表される。
ここで n は多角形の辺数、q は∠p/n　である。
k は n が倍になった回数、即ち n の倍加数。例えば　k = 2 の場合は、多角形の辺数は n x (2)2 ⇒ n x 4 となる。
アルキメデスは n = 6 の多角形から始めた。
その場合は次のようになる。
6(2)ksin((q/6)/2k) < p < 6 (2)k tan((q/6)/2k)

彼は多角形の辺数を 96(k = 4)まで増やし、次の結果を得た。
3 (10/71) < p < 3 (1/7)
または小数値で
3.14084 < p < 3.142858
計算が比率を使って行われたり（例えば3の平方根を265/153で置き換える等）、また彼の時代から千年も経った後になって三角法が発明されたことなどを考えると、これは非常に恐るべきことである。 


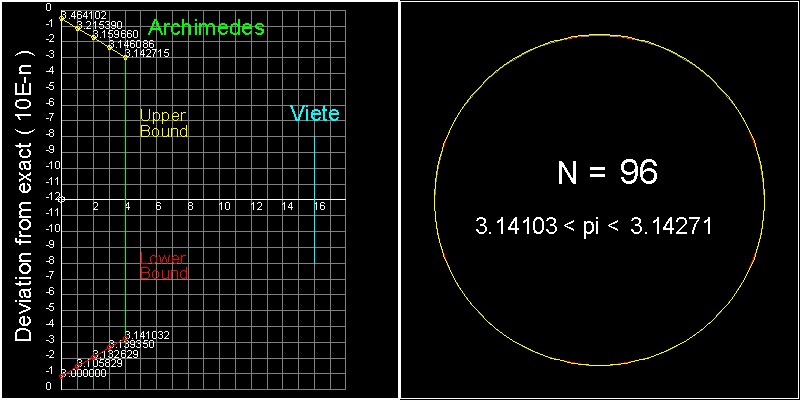
******************************** Archimedes_96_gon.dwg ********************************

ここをクリックしてアニメーションを見る。

この図面とアニメーションの作成方法：
   プログラム pi_approximation.lsp　を   (load "pi_approximation")　でロードする。
  次にコマンド ラインから Archimedes_pi 　と実行命令をタイプする。

ヴィエート(Viète) による改良

アルキメデスから約18世紀の後、イタリアの数学者フィボナッチ(Leonardo Pisano Fibonacci , 1170 - 1250) がアルキメデスと同じ96辺の多角形で小数点3桁(3.141)までを正した。次にフランスの数学者ヴィエート(Viète, 1540 - 1603) がアルキメデスのp近似に関する概念を三角法を用いて改訂し、k = 16におけるpの下限界と上限界を計算した。
これは393,216辺の多角形( 6 x 2 16 = 393,216)。
彼の結果は 3.1415926535 < p < 3.1415926537 である。
参考までに正確な値は 3.1415926535897932...。

ここをクリックしてアニメーションを見る。

この図面とアニメーションの作成方法：
   プログラム pi_approximation.lsp　を   (load "pi_approximation")　でロードする。
  次にコマンド ラインから List_pi_number 　と実行命令をタイプする。
反復回数は17を入力(repeat cycles=17)
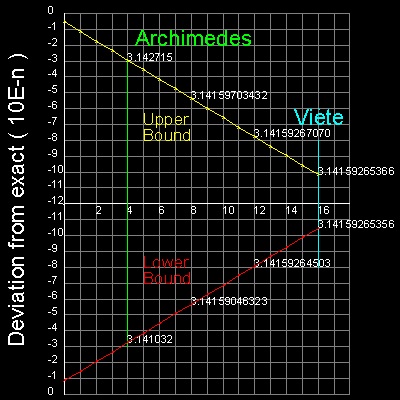
注） x 軸は整数kの線形、y 軸は底が10の対数。
kが4増加するごとに、上限界と下限界の値を表示。

上限界と下限界の線は何れも真っ直ぐで同じ勾配を持つ。
この説明を下記に述べる。
**************** Viete_pi.dwg ****************

線の勾配について

 
 sinxとtanxのマクローリン級数(Maclaurin series)
	sinx = x - x3/3! + x5/5! - ....		(1)
	tanx = x + (1/3)x3 + (2/15)x5 +  ....	(2)
下限界(LB) と上限界(UB) は
	LB = 6(2)k sin((p/6)/2k) 
	UB = 6(2)k tan((p/6)/2k
   ) 最初の2項を(1)と(2)に用いるとLBとUBは次のようになる
	LB = p[1 -(1/6)(p/6)2(2)-2k]
	UB = p[1 +(1/3)(p/6)2(2)-2k]
ここでLBとUBの正確なpの値からの偏りを定義：
	Fl = p - LB
	Fu = UB - p
よって
	Fl = (p/6)3 2-2k
	Fu = 2(p/6)3 2-2k
更に対数を取り
	log(Fl) = log(p/6)3 - (2log2)k			(3)
	log(Fu) = log{2(p/6)3} - (2log2)k		(4) 

(3)と(4)は y = a + bk　の線分方程式に相当する。
この方程式において、b は勾配、a はk = 0におけるy の値である。

ルーメン(Roomen)とルドルフ(Ludolph)による改良

1593年、ルーメン( Adriaan van Roomen, 1561 - 1615､ ラテン名 "Adrianus Romanus") は 230(= 1.07374x109) 辺の多角形で p の値を小数16桁まで求めた。彼の成果はルドルフ( Ludolph van Ceulen, 1540 - 1610) との交信が動機である。そして最終的には、ルドルフが p の値を35桁まで 262(= 4.61169 x 1018) 辺の多角形を用いて計算した。 

 
 内接および外接する多角形を用いたpの値のまとめ

	名前                              多角形の辺数	正確な値

アルキメデス(Archimedes, 287BC - 212BC)    96		3.14
フィボナッチ(Fibonacci, 1170 - 1250)       96		3.141
ヴィエート(Viète, 1540 - 1603)             6 X 216	10-th decimal place
ルーメン(Roomen, 1561 - 1615)              230		16-th decimal place
ルドルフ(Ludolph, 1540 - 1610)             262		35-th decimal place

参考文献

  1. Heath,Thomas L. :"History of Greek Mathematics Vol. I From Thales to Euclid" Dover 1981

  ホームページの内容目次に戻る  古代ギリシャ数学の三大問題  ギリシャ時代の円の求積

質問、問い合わせは 筆者 岩本 卓也宛てにお願いします。

Last Updated Nov 22, 2006

Copyright 2006 Takaya Iwamoto   All rights reserved. .