ホームページの内容目次に戻る   角の三等分    古典的な解

挿入法による古典的な解 (Neusis or Verging)

1. アルキメデスの挿入法（＃１）

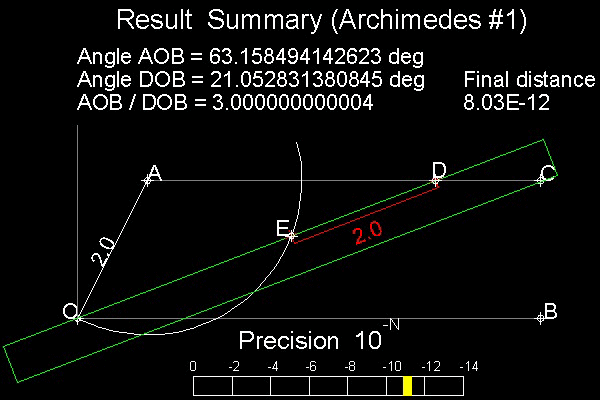
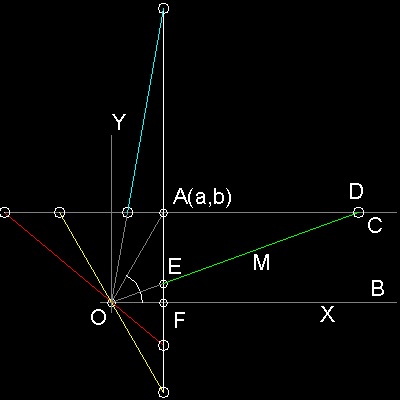
アルキメデスの方法を下図に示す。

証明:   AC と OB　は平行であるから
    ∠ADO = ∠DOB
三角形 AOE と AED は二等辺三角形であるから
    ∠ADE = ∠EAD
また　∠AOE = ∠AEO = 2 ∠ADE = 2 ∠DOB
従って　∠DOB = (1/3)∠AOB

************************* trisect_Archimedes_1.dwg *****************

ここをクリックしてアニメーションを見る。

この図面とアニメーションの作成方法：
  プログラム neusis.lsp を   (load "neusis")　でロードする。
  次にコマンド ラインから neusis_1 と実行命令をタイプする

挿入法（＃１）の代数方程式

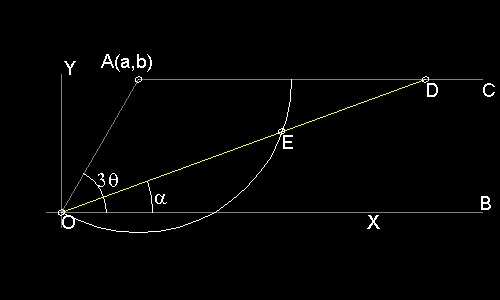
点A(a,b)　を中心とする円の方程式：
	(x-a)2 + (y-b)2 = a2 + b2
直線　AC :  y = b
直線　OD :  y = tanα x = mx
直線　OD　が　円、直線　AC　と交わる点を　E(x1,y1), D(x2,y2) とすると
	(ED)2 = (1 + m2)(x1 - x2)2 = a2 + b2
∠AOB = π/3 , AO = 1 とすると　a = 1/2, b = √3/2 となり
m についての４次方程式がえられる。
	f(m) = m4 - 4√3 m3 + 6m2 + 4√3 m - 3 = 0
この図面の作成方法：
  プログラム quartic_eqn.lsp を   (load "quartic_eqn")　でロードする。
  次にコマンド ラインから neusis_1_model と実行命令をタイプする

*********************** neusis_model_1.dwg **********************
この４次方程式　F(m)=0 の根を見つけるために　先ず　m = -2 から　6についてグラフにする。
Y軸の値は　25分の1 に縮小している。

この方程式を　解くと次の４個の解が得られる。 値の小さいほうから 
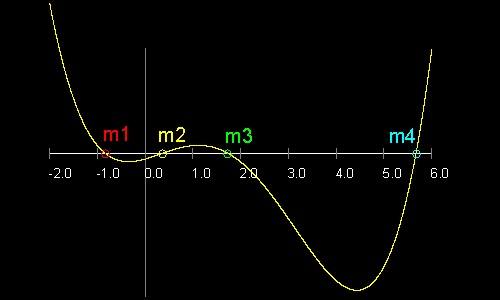
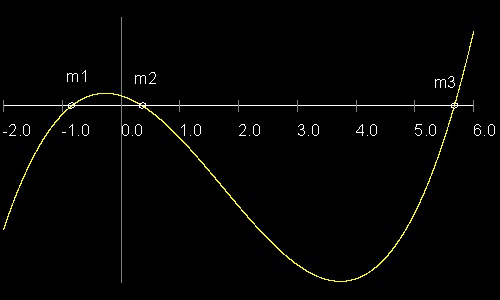
		tan α			α( ° )
   m1 = -0.83909963117728	-40.0000000000°
   m2 =  0.36397023426620	 20.0000000000°
   m3 =  1.73205080756888	 60.0000000000°
   m4 =  5.67128181961771	 80.0000000000°
この図面の作成方法：
  プログラム quartic_eqn.lsp を   (load "quartic_eqn")　でロードする。
  次にコマンド ラインから neusis_1_equation と実行命令をタイプする

****************** neusis_model_1_equation.dwg *****************
この４次方程式　F(m)=0 の根を見つけるには　ここでは　Newton-Raphson 法を使った。
筆者は　エクセル　をつかって　m2 を次のように計算した。
わずか4 回　の繰り返し計算で　少数以下　12桁まで正しく求められる。


********************************* neusis_1_equation_1.xls ********************************
この４次方程式　F(m)=0 の根　m1,　m2,　m3,　m4 を　使って　直線を引いてみよう。
見やすくするため、　m1(赤) ,　m2(黄色), m3(緑) ,m4(シアン) と色分けをしている。。

これを見てすぐに気がつくと思うが　m3(緑)の根は　無意味な解である。
m3 の値そのものを見てみると　これは　√3 の値で　tan(π/3)に等しい。
従ってこの４次方程式は　(m - √3)の因子を含んでいるので
次のようになる。 
(m - √3)(m3 - 3√3m2 - 3m + √3 ) = 0
これから　	m3 - 3√3m2 - 3m + √3　= 0
この式は　tan 関数の　３倍角公式から導かれるものであることを示そう。
この図面の作成方法：
neusis_model_1.dwg の図面をベースにしてm1~m4 の解の直線を引く。

*************** neusis_1_equation_all_solution.dwg ************** 
sin と　cos　の角度の和の公式は
	sin(α + β) = sinαcosβ + cosαsinβ
	cos(α + β) = cosαcosβ + sinαsinβ
これを使うと
	tan(α + β) = sin(α + β)/cos(α + β) = (tanα + tanβ)/(1 - tanα tanβ)
従って　　　　tan2α = 2tanα/(1-tan2α)
そして　　　　tan3α = (tanα + tan2α)/(1 - tanα tan2α) = (3 tanα - tan3α)/(1 - 3tan2α)
これを展開してまとめると　最終的に　次のようになる。
	(tanα)3 - 3(tanα)2tan3α - 3(tanα) + tan3α = 0
m = tanα　と置くと
	m3 - 3(tan3α)m2 - 3m + (tan3α) = 0
三等分しようとする　角度が　60° の場合は　tan3α = √3 であるから　三次方程式は次のようになる。
	F(m) = m3 - 3(√3)m2 - 3m + √3 = 0
これは　上述の挿入法で導かれた　多項式と同じものである。
	
参考のため　F(m)　のグラフを下に示す。

Y軸の値は　10分の1 に縮小している。

この方程式を　解くと次の3個の解が得られる。
値の小さいほうから 
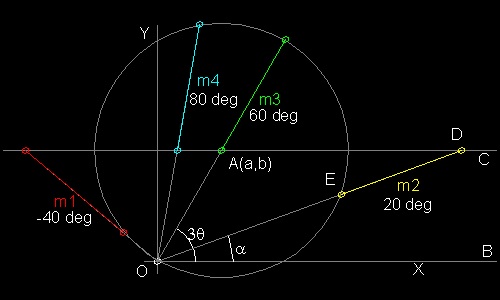
		tan α			α( ° )
   m1 = -0.83909963117728	-40.0000000000°
   m2 =  0.36397023426620	 20.0000000000°
   m3 =  5.67128181961771	 80.0000000000°
この図面の作成方法：
  プログラム quartic_eqn.lsp を   (load "quartic_eqn")　でロードする。
  次にコマンド ラインから neusis_1_equation_cubic と実行命令をタイプする

*************** neusis_1_equation_cubic.dwg **************

三個の解についての説明

例として　取り上げた　角度が　60度　であるから　その三等分の解が　20度　であるというのは　理解できる。
しかし　あと二個の角度　(-40度　と 80度 )については　少し説明を要する。
三角関数の値、例えば　tanθ は　θ に　2π, 4π を加えた角度 2π + θ, 4π + θ
においても同じ値を持つ。　だから　60度の三等分は同時に (360 + 60)度 , (720 + 60)度の三等分を意味する。
従って　140度 , 260度　も解になる。
m1 = -40　度　は　140 = 180 - 40; m3 = 80 度　は　360 - 80 = 260 に相当する。

2. パップス(Pappus)の挿入法

パップスの方法を下図に示す。 

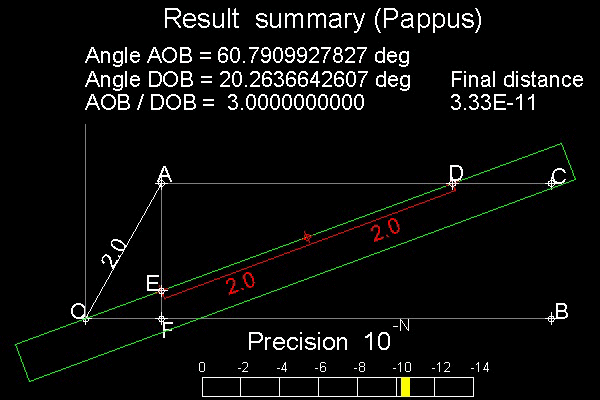
三等分の証明　:
∠EAD は 90 ° であるから、
3　点 A、D、 E は直径が ED の円上にある。
EDの中点を　M とするとM が　その円の中心点である。
従って　AM = (1/2)ED = AO = EM = MD
だから　ΔAOM と ΔMDA は、どちらも二等辺三角形である。
見方を変えると　
Aを中心に　半径　AO の円と直線　ODの交点がM である。
これは　アルキメデスの挿入方(#1) と同じ結果になる。
従って　直線　OD は　∠AOB　の三等分線である。

************************* trisect_Pappus_1.dwg*******************

ここをクリックしてアニメーションを見る。

この図面とアニメーションの作成方法：
  プログラム neusis.lsp を   (load "neusis")　でロードする。
  次にコマンド ラインから neusis_2 と実行命令をタイプする

パップス(Pappus)の挿入法の代数方程式

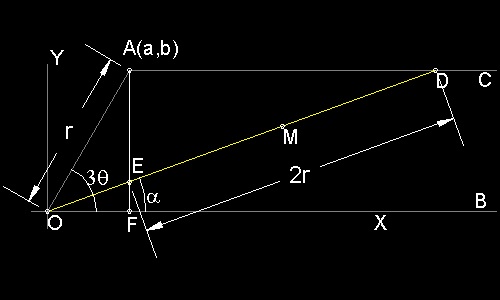
直線　AF :  x = a ; 直線　AC :  y = b
直線　OD :  y = tanα x = mx
直線　OD　が　直線　AF　,ACと交わる点を　E(x1,y1), D(x2,y2) とすると
(ED)2 = (x1 - x2)2 + (y1 - y2)2 = 4(a2 + b2)
x1 = a, y1 = ma; x2 = b/m, y2 = b
であるから
(a - b/m)2 + (ma - b)2 = 4(a2 + b2)
ここで　(b/a) = tan(3θ) と置き換え　、上の式を整理すると
F(m) = (m + tan3θ)(m3 - 3tan3θ m2 - 3m + tan3θ ) = 0
となり、　m についての４次方程式がえられるが　(m + tan3θ) = 0
が　解でないことは　明白であるから　、三等分の方程式は　
f(m) = m3 - 3tan3θ m2 - 3m + tan3θ  = 0
であたえられる。　
******************* neusis_model_2.dwg ****************** 
3θ = π/3 のとき　この式は　m3 - 3√3 m2 - 3m + √3  = 0
となる。　これは　アルキメデスの挿入方(#1) の場合と全く同じものである。
この４次方程式　F(m)=0 の根を見つけるために　先ず　m = -2 から　6についてグラフにする。
Y軸の値は　25分の1 に縮小している。

この方程式を　解くと次の４個の解が得られる。 値の小さいほうから 
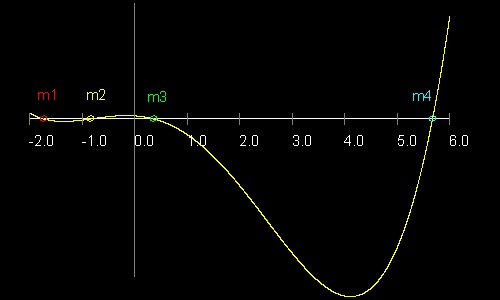
		tan α			α( ° )
   m1 = -1.73205080756888	-60.0000000000°
   m2 = -0.83909963117728	-40.0000000000°
   m3 =  0.36397023426620	 20.0000000000°
   m4 =  5.67128181961771	 80.0000000000°
この図面の作成方法：
  プログラム quartic_eqn.lsp を   (load "quartic_eqn")　でロードする。
  次にコマンド ラインから neusis_2_equation と実行命令をタイプする

****************** neusis_model_2_equation.dwg *****************

この４次方程式　F(m) = 0 の根　m1,　m2,　m3,　m4
を　使って　直線 y = mx を引いてみよう。
見やすくするため、m1(赤),m2(黄),m3(緑),m4(シアン)
と色分けをしている。
４次方程式であるから　
４個の根が　あるのは　予想できる。
求める解は　m3 (20°)　であり　m2, m4 も　解の一部であることは
すでに　上述した通りである。
しかし　m1 (- 60 °)　の持つ意味が　これだけの情報では理解できない。
そのためには　パップスが考え出した　
挿入点　ED　を見付ける一般的な手法を説明する必要がある。
それには、下記の
パップス(Pappus)による挿入法　の一般解法　を参照されたい。
*************** neusis_2_equation_all_solution.dwg ************** 
三次方程式は　アルキメデスの挿入方の場合と同じであるが	
参考のため　F(m)　のグラフを下に示す。

Y軸の値は　10分の1 に縮小している。

この方程式を　解くと次の3個の解が得られる。
値の小さいほうから 
		tan α			α( ° )
   m1 = -0.83909963117728	-40.0000000000°
   m2 =  0.36397023426620	 20.0000000000°
   m3 =  5.67128181961771	 80.0000000000°

*************** neusis_1_equation_cubic.dwg **************

パップス(Pappus)による挿入法　の一般解法

パップスは二つの直線にまたがって、与えられた長さの線分を挿入する一般的な手法を考えだした。
それは　ユークリッド　の　幾何原論　の　第一巻にある定理 43 と　彼の時代に既に良く知られていた
円錐曲線の一つである　双曲線を使ったものである。　以下にそれを簡単に説明する。
　 挿入法の問題は次のように表される。
ABCD は平行四辺形である。　A を通る直線が　CD　と BC　の延長と交わる点を　 E,F
とするとき　EF があたえられた長さになるようにする。
定理 43 を簡単に言うと　"BIEC とEDHJ　の面積は等しい。"
ABCD = IBCE + AIED , AIJH = DEJH + AIED
であり、　AIED は共有されているから
ABCD = AIJH
従って　 BC x CD = BF x ED
FH　上に点G を取り　平行四辺形　EDGF　を作る。
ED = FG　であるから　BF x ED = BF x FG
故に　BC x CD = ab = BF x FG = 一定値

点G は　BCを x 軸、 BAを y 軸としたとき,
xy=ab なる双曲線　と 点D を中心として
与えられた長さを半径とする円弧の交点である。

*************** verging_generalized.dwg **************
この図面の作成方法：
  プログラム quartic_eqn.lsp を   (load "quartic_eqn")　でロードする。
  次にコマンド ラインから draw_hyperbola と実行命令をタイプする

例　:   60° の場合 

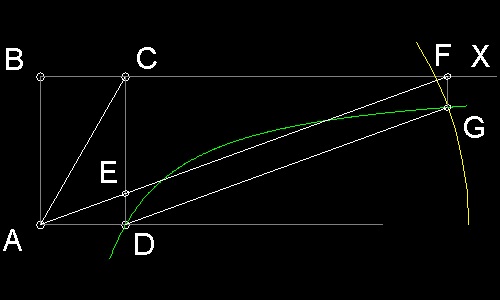
三等分する角度　∠CAD = 60 °　であるから
AD = BC =1, AB = CD = √3 , AC=2.0 である。
xy = ab = √3 の双曲線を　緑色で示す。
点D を中心として半径 4.0 の円との交点を　G とする。

G から BCに垂線を下ろした点　が　F である。
AF が　∠CAD　の三等分線である。
この図面の作成方法：
  プログラム quartic_eqn.lsp を   (load "quartic_eqn")　でロードする。
  次にコマンド ラインから pappus_example と実行命令をタイプする
結果の図面を　一部だけ取り出す。
*************** 60_deg_case_solution.dwg **************

   60° の場合ー総ての解 

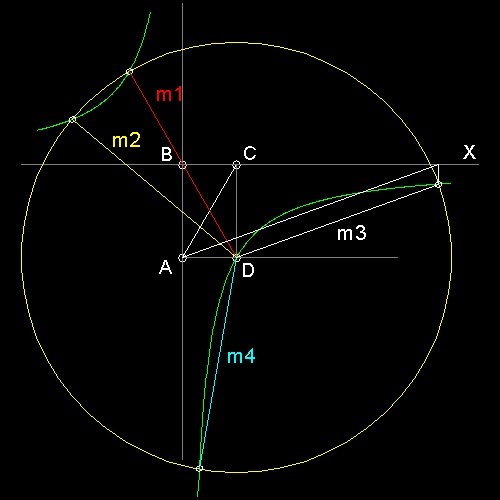
左図に示すように　双曲線と円の交点は　４個あることがわかる。
それは挿入法の解が　４次方程式の根であることからも推測できる。
　　　その　４個の解は　
	　　m1 = -60°
	　　m2 = 140°　= (360/3)° + 20°
	　　m3 =  20°
	　　m4 = 260° = (720/3)° + 20°
　　　である。
　m1 は無意味な解であるので　m2, m3, m4 が三個の解である。
この図面の作成方法：
  プログラム quartic_eqn.lsp を   (load "quartic_eqn")　でロードする。
  次にコマンド ラインから pappus_example と実行命令をタイプする
結果の図面を　修正を加える。
*************** 60_deg_case_all_solution.dwg **************

3. アルキメデスの挿入法（＃２）

アルキメデスの方法を下図に示す。

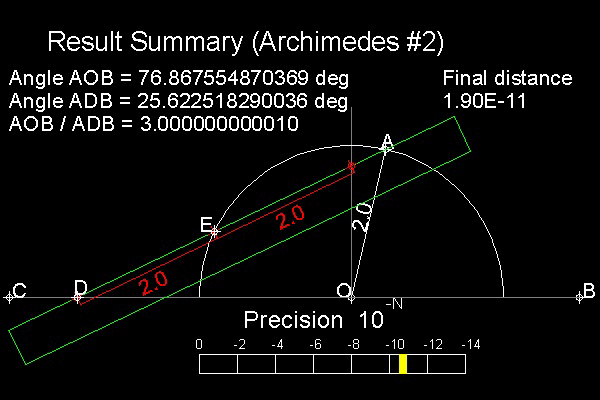
アルキメデスの挿入法（＃1） の　
上下を逆にすると　このモデルになる。

従って　説明は上記を見てください。

このモデルは　コサイン　を未知数にした　
与えられた角度　が　3θ の　三等分方程式
    X3 - 3X - 2a = 0
ここで　X = 2cosθ ;   a = cos3θ である。

につかわれている。
************************* trisect_Archimedes_2.dwg *******************

ここをクリックしてアニメーションを見る。

この図面とアニメーションの作成方法：
  プログラム neusis.lsp を   (load "neusis")　でロードする。
  次にコマンド ラインから neusis_3 と実行命令をタイプする

参考文献

1. Yates,Robert Carl : "The Trisection Problem", NCTM, 1971.

2. Heath,Sir Thomas L. : "A History of Greek Mathematics", Vol. 1, Dover, 1981.

ホームページ の内容目次に戻る   角の三等分    古典的な解

質問、問い合わせは 筆者 岩本 卓也 宛てにお願いします。

Last Updated Nov 22, 2006

Copyright 2006 Takaya Iwamoto   All rights reserved.