 三等分の仕方と手順:
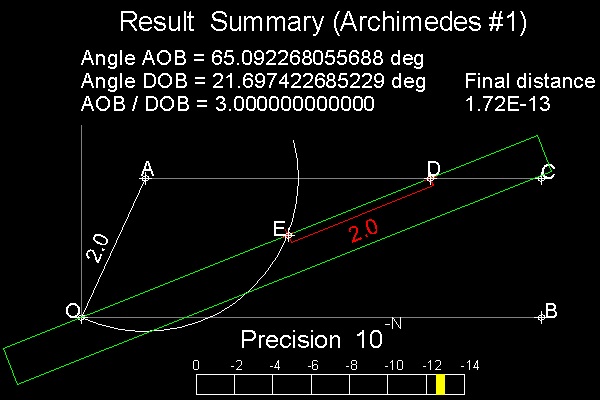
三等分の仕方と手順: 1.座標原点 (0,0) の点 O から 距離が 2.0 の点A を決める。
Aを中心にして半径 2.0 の円を描く。
∠AOB を三等分する角とする。
線分OB に平行な線分AC を引く。
2. 距離が 2.0 になるように点E, D に目印をした定規(緑線)を用意する。
3. 図のように定規の辺が点O を通り、点Eがその円上にくるように定規を
移動させる。
4. さらに,そのとき点 D が線分AC上に来るようにする。
アルキメデスの方法を下図に示す。
 三等分の仕方と手順:
三等分の仕方と手順:
1.座標原点 (0,0) の点 O から 距離が 2.0 の点A を決める。
Aを中心にして半径 2.0 の円を描く。
∠AOB を三等分する角とする。
線分OB に平行な線分AC を引く。
2. 距離が 2.0 になるように点E, D に目印をした定規(緑線)を用意する。
3. 図のように定規の辺が点O を通り、点Eがその円上にくるように定規を
移動させる。
4. さらに,そのとき点 D が線分AC上に来るようにする。
ここでは点 D と線分AC との距離をできる限り小さくする努力をする。
点D が線分ACの真上に来れば(即ち点D と線分AC
との距離
がゼロになれば)三等分は完了。そのとき
AC が OBと平行であり、ΔAOE, ΔAED が二等辺三角形であることから
OD が ∠AOB の三等分線であることがわかる。
しかし、有限回数の操作でゼロにすることは不可能である。
三点 O,E,Dで別々に拘束を与えることは出来ない。 二点O,Eで拘束
すれば 点D は決まってしまうからである。実際には D と線AC
の距離が 或る値以下になったところで操作を打ち切らねばならない。
************************* trisect_Archimedes_1.dwg
*****************
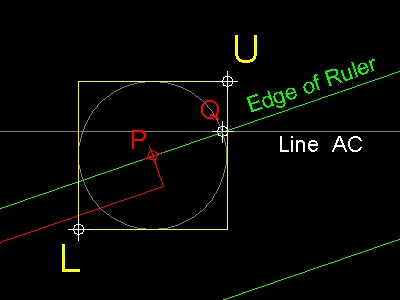 点 D が線分 AC
に限りなく接近するのを確かめるようにするには、
点 D が線分 AC
に限りなく接近するのを確かめるようにするには、
画面上のマウスの動きに対して精度が維持できるよう、
自動的に画面が拡大(ズーム)できるようにすると良い。
筆者のアイデアは次の通り:
1. ウィンドウをグローバル表示と拡大表示のウィンドウの2つに分割する。
2. マウスを左クリックして位置(P)を決めると、新しいウィンドウの境界(L と U)
が半径PQ によって計算される。 Qは線分AC と定規の辺(緑線)との交点。
この部分の表示は細かいので境界位置の値によって自動的に拡大する。
3. 操作中の距離PQ の精度確認は、グローバル表示用ウィンドウの下方にある
精度表示板(precision bar)で見ることができる。この操作は 1.e-10 の精度まで行える。
*************** auto_zoom.dwg **************

************************* neusis_1_zoom.dwg
*******************
この図面とアニメーションの作成方法:
プログラム neusis.lsp を
(load "neusis") でロードする。
次にコマンド ラインから neusis_1 と実行命令をタイプする。
パップスの方法を下図に示す。
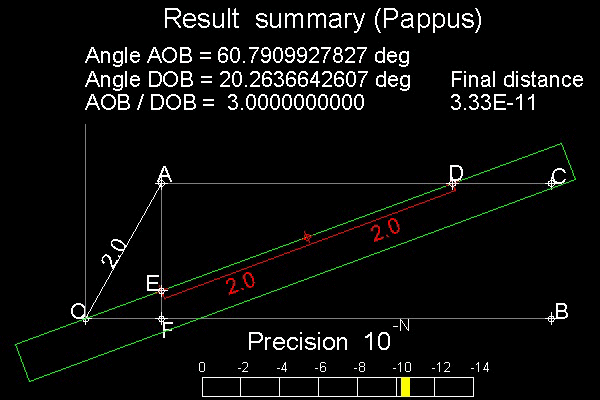 三等分の仕方と手順:
三等分の仕方と手順:
1.半径2の円を描く。
円上の点Aを定める。
∠AOB を三等分する角とする。
線分OB に平行な線分AC を引く。
線分OB に垂直な線分AF を引く。
2. 距離が 2.0 x 2 になるように点E と点D に目印をつけた定規(緑線)
を用意する。
3. 図のように定規の辺が点O を通り、点E が線分AF上に位置するように
定規を移動させる。
4. さらに点D が線分AC の上に来るように定規を移動させる。
ここでは点D と線分AC との距離をできる限り小さくすること。
************************* trisect_Pappus_1.dwg
*******************
この図面とアニメーションの作成方法:
プログラム neusis.lsp を (load
"neusis") でロードする。
次にコマンド ラインから neusis_2 と実行命令をタイプする。
詳しくは パップス(Pappus)の挿入法の章で説明。
アルキメデスの方法を下図に示す。
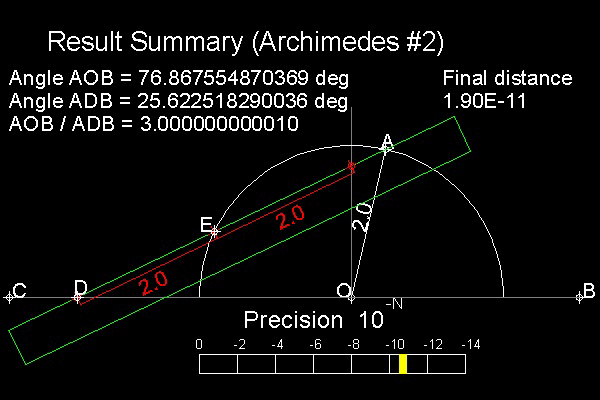 三等分の仕方と手順:
三等分の仕方と手順:
1.半径 2.0 の円を描く。
円上の点Aを定める。
∠AOB を三等分する角とする。
2. 距離が 2.0 になるように点E と点D に印をした定規(緑線)を用意する。
3. 図のように定規の辺が点A を通り、点Eがその円上にくるように定規を移動させる。
ここでは点D と線分BC との距離をできる限り小さくするように努力する。
パップスの方法との類似性を示すために、パップスが使用した定規と
同じものを(逆さにして)使用した。
************************* trisect_Archimedes_2.dwg
*******************
この図面とアニメーションの作成方法:
プログラム neusis.lsp を (load
"neusis") でロードする。
次にコマンド ラインから neusis_3 と実行命令をタイプする。
三等分の方程式は二次項( X 2 ) の無い三次多項方程式である。
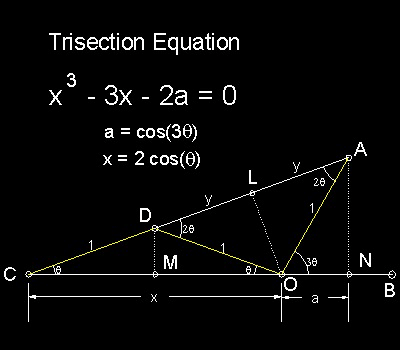 これは、角の三等分が目盛りの無い定規とコンパスのみを使って
これは、角の三等分が目盛りの無い定規とコンパスのみを使って
立方根の値の長さの線を描くのに等しいことを意味する。
このことが不可能であることについてヴァンツェル(Wantzel)が 1837年に論文を発表した。
******** trisection_equation_desc.dwg
*********
代数による表現:
3つの三角形 CDM、COL、CAN は相似、よって CM/CD = CL/CO = CN/CA となる。
そこで x/2 = (1 + y)/x = (x + a)/(1 + 2y) から
⇒ x2 = 2 + 2y と 1 + 2y = 2(x + a)/x を得る。
ここで双方の y を消去すると、 x 2 - 1 = 2(x + a)/x または x 3 - 3x - 2a = 0 となる。
(但し、x = 2cos(q) 、 a = cos(3q) である。)
詳しくは 三等分方程式の章で説明。質問、問い合わせは 筆者 岩本 卓也 宛てにお願いします。
Last Updated Nov 22, 2006
Copyright 2006 Takaya Iwamoto All rights reserved.