特殊曲線

特殊曲線を使った角の三等分

デカルト(René Descartes)の放物線(Parabola)

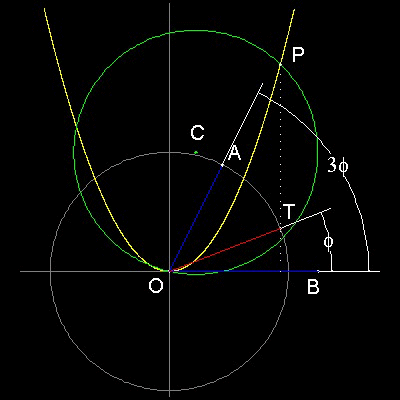
デカルト(René Descartes , 1596 - 1650) は放物線を使って角の三等分を示した。デカルトの方法を下記に示す。

デカルトの「幾何学」(La Géométrie)

デカルトの「幾何学」(La Géométrie )英訳引用文：

「数学者が、科学の分野で偉大な画期的な業績をあげた者
の名を挙げろと問われれば、きっと１９世紀については答え
られないだろう。１８世紀についても同じだろう。しかし１６世紀
と１７世紀、特に古典ギリシャ時代の業績については、
はっきり云えるだろう。ギリシャ文明の中ではユークリッド、
アルキメデス、アポロニウスは必ず含まれるだろうし、
１７世紀の数学大ルネサンスに貢献した中ではデカルトの
「幾何学」(La Géométrie) とニュートンの「原理」(Principia)
が必ず含まれるだろう。」
******** parabola_tri_desc.dwg ********

デカルトは、デリアンと三等分の問題は三次元方程式の解に等しく、
その解が円錐曲線（その内一つが放物線）を使って得られることを示した。

角の三等分では三等分方程式の根： x³ - 3x -2a = 0 , 但し a = cos(3q ) 、は
(1)放物線
と
(2)点(a, 2)を中心とする円の交点の x 座標値で表される。
故に
(1) y = x²

(2) x² + y² - 2ax - 4y = 0

(1) を (2)に代入して　y を消去すると、x のみの方程式は

x ( x³ - 3x -2a ) = 0 , または x³ - 3x -2a = 0

となる。

この図面とアニメーションの作成方法：
プログラム parabola_trisection.lsp を (load "parabola_trisection")　でロードする。
次にコマンドラインから parabola_trisection と実行命令をタイプする。

ユーザに三等分する角を決めさせ、放物線と円を描く。その他の操作は手動でできる。
例： ∠AOB = 60度の場合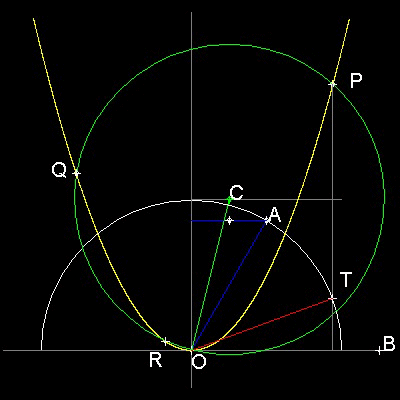
1.@2<60 と入力し、点Aを指定。
2. 点A から y軸へ垂線（青線）を引き、その中点を標す。
3. その中点を通る垂線に平行な線分 y=1 上の点C を求める。
4. 点C を中心に半径CO の円（緑円）を描く。
5. 緑色の円と黄色の放物線の交点を P, Q, R とする。
6. 点P からx軸に垂直に線を引く。
7. この線が単位円と点T で交差する。
8. ∠TOB が∠AOBの三等分角である。
問：点Q と点R はどうでしょう？
** parabola_trisection_60_deg_case.dwg **

ホームページの内容目次に戻る角の三等分特殊曲線

質問、問い合わせは筆者岩本卓也宛てにお願いします。

Last Updated Nov 22, 2006