特殊曲線

特殊曲線を使った角の三等分

1. 円積曲線(Quadratrix) - ヒピアス(Hippias)

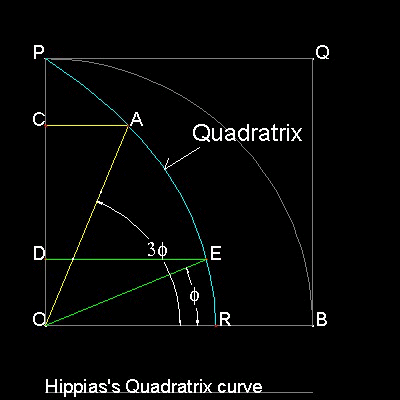
ヒピアス(Hippias, 約460BC ~ 400BC)の三等分法を下図に示す。角の三等分問題を解くために最初に考え出された曲線が
、なんといきなり所謂、超越関数と呼ばれるものであったことは興味深い。　この発明が当時のギリシャ世界で如何に画期的
なものであったことは、発明者　ヒピアスは　これにより一躍有名になり、各地を講演旅行してまわり、経済的にも裕福であった
とつたえられていることからも推測できる。ただし　同時代の数学者(たとえば　プラトン )からは　その言行について　いささか
冷ややかに批評されている。多少はやっかみもあろのであろう。
この曲線の名前　quadratrix　は円積問題(circle quadrature)を解くための曲線(-trix) という意味である。
その理由は、この曲線を使って円周率を見つけることが出来るからである。
そのことに　だれが最初に気が付いたかにつては　諸説がある。
ひとつは　ヒピアス　はすでに　知っていたという説、もうひとつ　は彼の死後　メナケムス
の弟　デノストラトス(Dinostratus) 約390BC ~ 約320BC) によるものであるという説の二つである。　しかし、
どちらが正しいかは別にして、この曲線はもともと角度の三等分、さらに一般的な　N 等分に使うために発明されたものである。

三等分の仕方：

ステップ 1：円積曲線を描く。曲線上の点A を指定し∠AOBを定義。

ステップ 2：点A からOB に平行な線を引き POと交差する点をC とする。

ステップ 3：線分CO 上でOD = CO/3 となる点D を求める。

ステップ 4：点D からOB に平行な線を引き曲線との交点をE とする。

∠EOB は∠AOBを三等分した角である。

*********** quadratrix_tri_desc.dwg ***********

ここをクリックしてアニメーションを見る。 詳しくは円積曲線 - ヒピアス(Hippias)の章で説明。

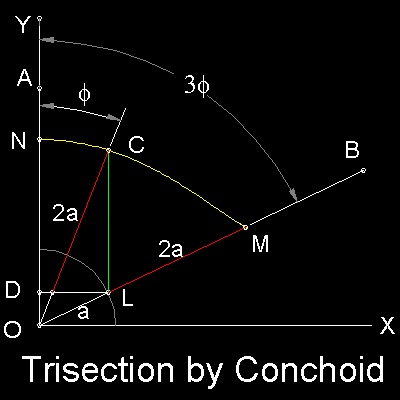
2. コンコイド(Conchoid)－ニコメデスが発明(Nicomedes)、パップスが使用(Pappus)

コンコイドを用いた角の三等分を下図に示す。
この曲線は初めコクロイド (Cochloid) と呼ばれ、後にコンコイド (Conchoid) と呼ばれるようになった。
"貝殻の形をした曲線"という意味で　ギリシャ語　の　conch, cockle (貝殻)に接尾語　の　-oid (--の形をした）の合成語である。
コンコイドは、ニコメデス (Nicomedes, 約280 BC - 約210 BC) がデリアン問題 (Delian Problem)を解くために発明した。
その後パップス Pappus of Alexandria (約290 - 約350) が角の三等分にも使用できることを示した。

三等分の仕方：

ステップ 1 : 直角座標軸O-XYを描き、OY上に点Aを定める。
図のように線分OB を引き、三等分する角を∠AOBとする。

ステップ 2 : 点O を中心に半径(a)の円を描く。
円と線分OBの交点をLとする。LからX軸に平行な線を引き、
Y軸との交点をDとする。

ステップ 3 : Oを基点にしたポールを想定し、線分DLと交わる点
からの長さが常に2aとなるような曲線NCM　(黄色で示す)、
コンコイド(Conchoid)を描く。

ステップ 4 : 点L からY軸に平行な線を引き、コンコイドとの交点を
Cとする。線分OCは∠AOBを三等分する。

******** conchoid_trisection_desc.dwg ********

ここをクリックしてアニメーションを見る。 詳しくはコンコイド - ニコメデス(Nicomedes)の章へ。

3. アルキメデスの螺旋(Archimedes' Spiral)

アルキメデス(Archimedes of Syracuse , 287 BC - 212 BC) は角の三等分に螺旋を用いた。
これをアルキメデスの螺旋(Archimedes' Spiral)という。アルキメデスの方法を下図に示す。

三等分の仕方：

1. アルキメデスの螺旋 r = a θ を描く。
2. 図のように点Aを指定し三等分する角を∠AOBとする。
3. 線分OAと螺旋との交点をPとする。
4. 線分OPを OQ = (1/3)*OP となるように三等分する。
5. 点Oを中心とし半径OQの円を描く。

6. 円と螺旋の交点をEとする。
∠EOB = (1/3) ∠AOBである。

************* spiral_tri_desc.dwg *************

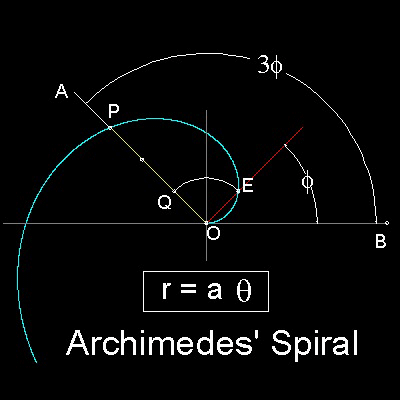
ここをクリックしてアニメーションを見る。　詳しくは螺旋 - アルキメデス(Archimedes)の章へ。

4. 双曲線(Hyperbola) - パップス (Pappus)

パップス (Pappus of Alexandria , 280 - 350) は双曲線が角の三等分に使用できることを示した。パップスの方法を下図に示す。

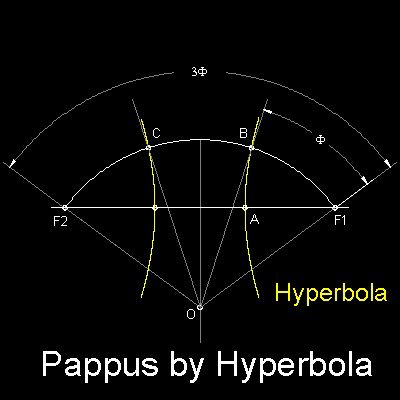
∠F₁OF₂ の三等分は、弧 F₁-F₂ を三等分するのに等しい。
これは離心率２の双曲線で達成できる。
双曲線上の全ての点において、F₁（焦点)からの距離が
Y軸 (準線)への法線距離の２倍であることを意味する。
また線対象であることから、交点B と交点C は
弧 F₁-F₂ を三等分する。
******** Pappus_hyperbola_tri_desc.dwg ********

ここをクリックしてアニメーションを見る。 詳しくは双曲線 - パップス(Pappus)の章へ。

5. 蝸牛形ーリマソン(Limaçon) - パスカル(Pascal)

ここで言う　パスカル(Pascal)　は　エチエンヌ　パスカル Etienne Pascal , 1588-1651 ) のことで
, 数学の世界の　"パスカルの三角形"、"パスカルの定理 ", 確率論　、そして　物理学の世界で
圧力に関する"パスカルの定理 ",(気象予報で使われる気圧の単位が　パスカルとよばれるのはそのためである。）、
そして　哲学の世界でも　有名な著作を残した 17世紀のフランスの数学者、物理学者、哲学者
ブレーズ　パスカル(Blaise Pascal , 1623 - 1662 ) の父親　である。
一般に単に　パスカルと言えば　息子の　ブレーズ　パスカル　のことを指す。
エチエンヌ　パスカル　は国王のために税金を徴収する中級官吏であったが　数学、科学に興味を持ち
真空の実験を息子のブレーズとやったり、当時の一流の数学者の集会に息子を連れて行ったりした。
このことが　後にブレーズの研究の役に立ったことは間違いない。
ブレーズが機械による計算機を発明したのは　父親が計算で苦労しているのを見かねた息子の
親孝行の現れであろう。

リマソン(Limaçon)は　1650年頃　エチエンヌ　パスカルによって発明され、
ニュートン( Isaac Newton , 1643 - 1727) によって角の三等分に使用された。パスカルの方法を下図に示す。

リマソンの描き方

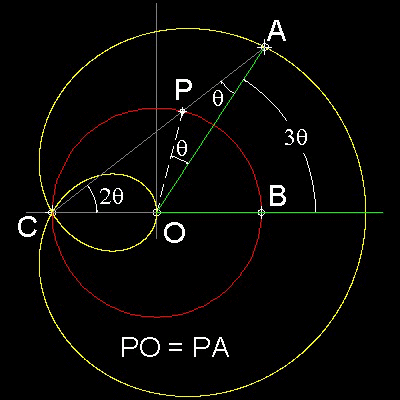
点Pは半径COの単位円に沿って移動。長さbは固定値とする。
線分CPの延長線上の点Aが PA = b となるように指定する。
点Pが単位円に沿って移動する時の点Aの軌跡が
リマソン(Limaçon)と呼ばれる曲線である。
三等分に使われるリマソンは b = 1 の場合である。
図の黄線は三等分に用いるパスカルのリマソン。

三等分

点Oを中心に単位円を描く。 b = 1 のリマソンを描く。

リマソン上の点Aを選択し、∠AOBを三等分する角とする。

線分CAを引く。 ∠CAOが三等分した角である。
******** limason_tri_desc.dwg ********

ここをクリックしてアニメーションを見る。　詳しくは蝸牛形 - パスカル(Pascal)の章へ。

6. デカルト(René Descartes) の放物線 (Parabola)

デカルト(René Descartes, 1596 - 1650) は解析幾何学の創始者と呼ばれている。1637年に有名な論文"La Géométrie"を出版した。
この本の中で、彼は放物線を使って角の三等分ができることを示した。デカルトの方法を下図に示す。

三等分の仕方

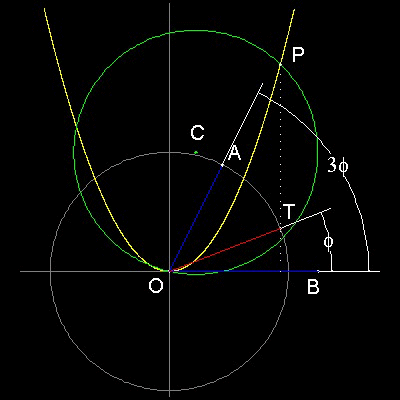
1. 半径 = 2の円を描き、点Aを定める。
    ∠AOBを三等分する角とする。　
 
2. AからOBに垂線を下ろす。その長さを 2a とする。
  　これは三等分方程式の2a に相当する。　
 
3. 放物線 y = x²を描く(黄)。
   また点C (a,　2)　を中心に原点を通る円を描く(緑)。　
 
4. 放物線との交点Pを求め、垂線をOBに下ろす。
　　この垂線とステップ1で描いたOを中心とする円
　　との交差点をTとする。　
 
5. 線分OTは∠AOBを三等分する。

******** parabola_tri_desc.dwg ********

ここをクリックしてアニメーションを見る。　詳しくは放物線 - デカルト(René Descartes)の章へ。

7. 三次放物線(Cubic Parabola)

放物線の方法は三次放物線に簡単に拡張できる。この方法を下図に示す。

三等分の仕方

1. 半径が　１と２の円を描く。三次放物線 y = (1/2) x ³を描く。
　直線 y = 3x/2 + 3 を引く。

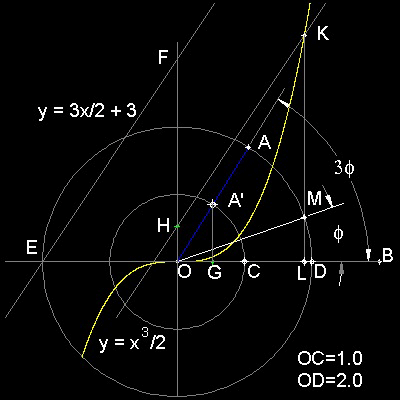
2. 外円上の点Aを指定し∠AOBを三等分する角とする。
OAが内円と交差する点をA'とする。点A'からOBに垂線を下ろし、
その交点をGとする。
注）長さOGは三等分方程式のa である。

3. OH = OG となるようにY軸上の点H を求める。
点H を通り線分 EF に平行な線を引く。

4. この直線は三次放物線と点Kで交わる。この点から
OBに垂直な線を下ろすと、点Mで外円と交差する。
線分MOが∠AOBの三等分線である。

******** cubic_parabola_tri_desc.dwg ********

ここをクリックしてアニメーションを見る。　詳しくは三次放物線の章へ。

8. チェバ (Ceva) のサイクロイド(Cycloid)

チェバ (Tomasso Ceva, 1648 - 1737)は　はチェバの定理で知られているジョヴァンニ・チェバ ( Giovanni Ceva , 1647 - 1734)
の弟である。アルキメデスの挿入法を、Cycloidum anomalarum と名付けた特殊曲線（チェバのサイクロイド）を用いて
与えられた任意角の三等分に応用した。

チェバの方法を下図に示す。

三等分の仕方

1. チェバのサイクロイドを描く（ アニメーション参照）

2. 三等分する角 ∠AOBを定義

3. 線分OA上の単位長OEを求める。点Eを通り線分OBに平行な線を引く。

4. この線分によりチェバのサイクロイドを６箇所切断。P、S、T は
それぞれ角 3θ 、360° + 3θ 、 720° + 3θ で三等分角。

残りの３点 P'、 S'、T' は 3θ を　180 - 3θ　で置き換えた場合の解である。
******** cycloid_of_Ceva_tri_desc.dwg ********

ここをクリックしてアニメーションを見る。　詳しくはCycloidum Anomalarum - チェバの章へ。

9. マクローリンの三等分曲線 (Maclaurin's Trisectrix)

マクローリン(Colin Maclaurin , 1698-1746) はマクローリン級数で知られているスコットランドの数学者である。
わずか　１１歳で　グラスゴー大学に入学を許され、その一年後には　独力で　ユークリッドの　"幾何学原論"　
全１３巻　の内　６巻を完全にマスターしたと言われている。　そこで　数学の教授をしていた　"シムソン線"　
で有名な　ロバート　シムソン(Robert Simson)と出会い　ギリシャ古典幾何学に興味を持つようになった。
数学の物理学への応用にも優れ　二度にわたり　フランス科学アカデミー　から賞を獲得している。
一回目は　"物体の衝撃について" ,二度目は　"潮汐について" で二回目の賞は　当時を代表する　二大数学者
オイラー(Euler)　、　ダニエル　ベルヌーイ(Daniel Bernoulli)　との連名受賞であることからも
かれが　当時の一流の数学者であったことがわかる。

彼はマクローリンの三等分曲線(Maclaurin's Trisectrix) と呼ばれる曲線を使って、与えられた角度の三等分を行った。

マクローリンの方法を下図に示す。

三等分曲線の描き方

1. 点Oを中心とし単位半径の半円BCを描く。
線分EFはCOの垂直二等分線である。

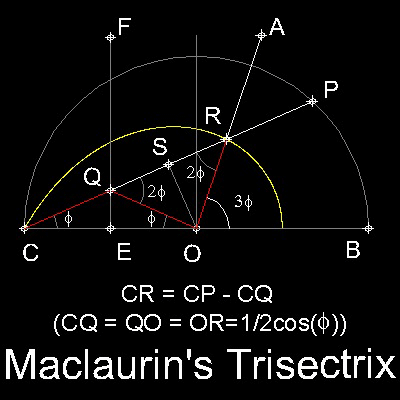
2. EF上の点Qを指定する。
線分CQの延長線と半円の交点をPとする。

3. CR = CP - CQを満足する点Rを求める。

4. 点Qが線分EFに沿って移動する際に描かれるRの軌跡を
マクローリンの三等分曲線という。

注） QがEFに沿って移動することから、この方法を
"imaginary" リンク CQ-QO-OR とも言う. リンクの長さが変数で
実際には存在しないので "imaginary" （想像上の）と呼ばれる。
******** Maclaurin_tri_desc.dwg ********

三等分の方法

この曲線は∠ROBが∠QCBの３倍となる性質がある。　従って曲線を描けば角度の三等分は明らかである。
ここをクリックしてアニメーションを見る。 詳しくは三等分曲線 - マクローリンの章へ。

ホームページの内容目次に戻る角の三等分

質問、問い合わせは筆者岩本卓也宛てにお願いします。

Last Updated Nov 22, 2006