直線運動の場合
このページにあるアニメーションのリスト(ハイパーテキストをクリックするとアニメーションがみられます。)
ここにもどるにはブラウザーの"Back" ボタンを使う。
| 直線追跡 -- k = 1.5 の場合 k = 1.5 の場合 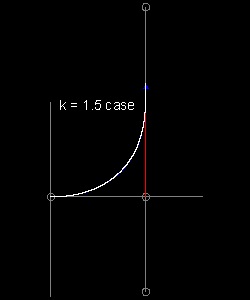 |
直線追跡 -- k = 1.0 の場合 k = 1.0 の場合 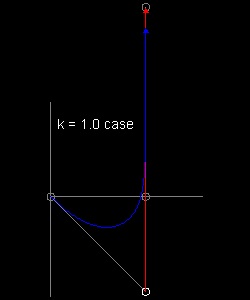 |
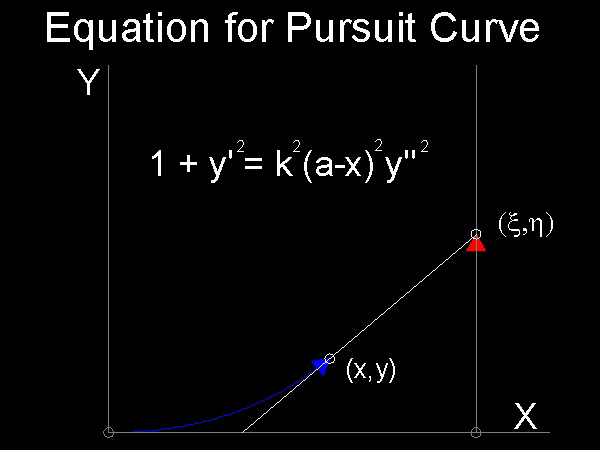
下図を参照しながら 追跡する犬のたどる軌跡を求める方程式を導こう。
これは追跡曲線が直線上を移動する場合である。うさぎがx-軸の休憩点から直線 x = a 下図)に沿って追跡されるとする。
同時に犬が原点からうさぎのk倍の速度で追跡すると、
ξ = a, (η - y)/(a - x) = y' または
η = y + (a - x)y'
dx2 + dy2 = k2(dξ2 + dη2) = k2 dη2
更に: dx2 + dy2 = k2*[dy - y'dx +(a-x)dy']2
= k2(a-x)2(dy')2
または 1 + y'2 = k2(a-x)2y''2
これは y' = p と 置いて p について解くことのできる微分方程式である。[2, 4, 5]
******************
pursuit_curve_equation.dwg
*******************
出力の例
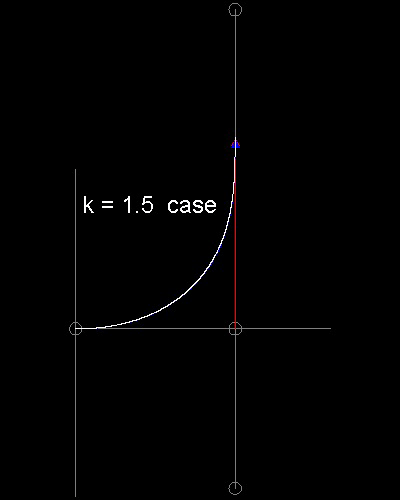
********** linear_pursuit_1.dwg *********** ********** linear_pursuit_2.dwg ***********
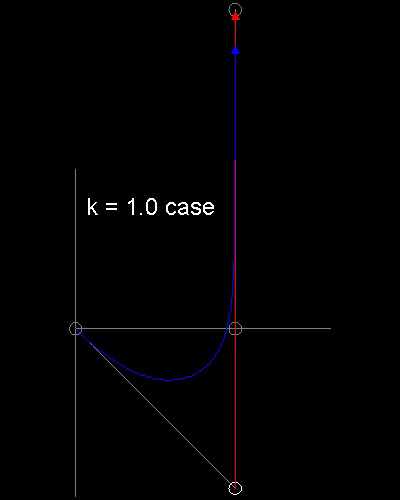
k = 1.5 の場合 ここをクリックしてアニメーションを見る。 k = 1.0 の場合 ここをクリックしてアニメーションを見る。
この図面とアニメーションの作成方法:プログラム pursuit.lsp を (load "pursuit") でロードする。
次にコマンド ラインから pursuit_linear と実行命令をタイプする。
k=1.5 の場合、 k=1.5 に設定しその他の入力は既定値を用いる。
k=1.0 の場合、 うさぎのスタート地点は(5,-5)
注*: このプログラムは red_arrow.dwg と blue_arrow.dwg が必要です。
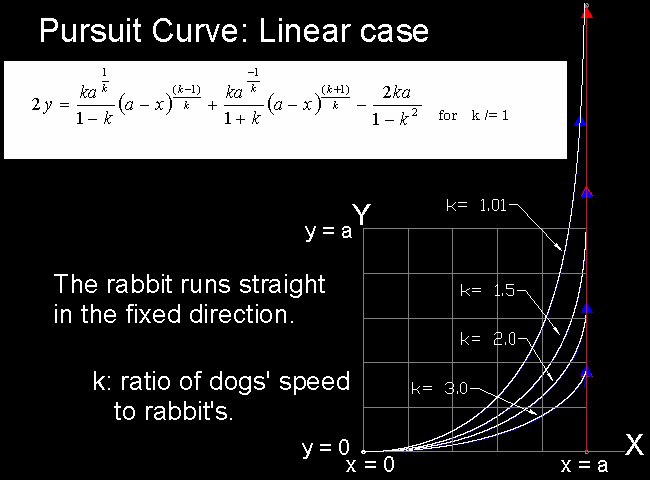
k の値を1.01 から 3.0に変化させてみた場合の結果をまとめてを次に示す。
************************** pursuit_linear_1.dwg **************************
既定の入力値は、うさぎが(5 , 0)点 からスタートし、犬が(0 , 0)点から追跡し始めるように設定してある。
相対速度の既定値は2.0に設定してある。
この実行命令は一般の追跡曲線問題に使える基本的な関数を持ち、
うさぎが円上を走る場合( 円の上を追跡する場合)と、
犬が楕円上の点から出発しうさぎが楕円の一焦点から楕円の原点へ向けて走る場合(
楕円上の点から追跡する場合 )、
の両方プログラムのテンプレートとしてもつかえるように開発されている。