立方体の倍積問題
 ホームページの内容目次に戻る  古代ギリシャ数学の三大問題  デリアン問題

その後の数学者

1. ニコメデス(Nicomedes) revisited

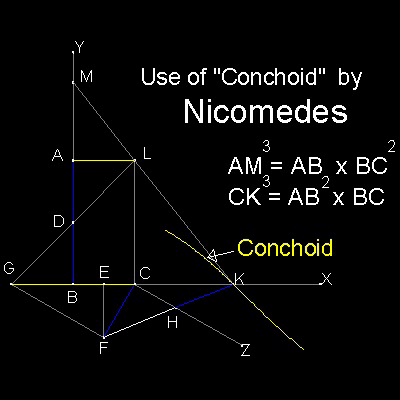
ニコメデス(Nicomedes)の解の核心は、線分CZ とCX が交差する点K をneusis process (verging)で求めることである。

二つの与えられた線分のデータは、BC とCF (= AD = HK)であることを意味する。

AM = FH であるから、引数に必要な全要素は、B,C,E,F,G,H,K,Zで作られる図形に含まれる。

点A,L,D,Mで結ばれた図形は余計に見える！！
********* Nicomedes_Delian_desc.dwg ********

その後の数学者達は（誰だか判らないが）これに気付き、ニコメデスのデリアンモデルを次のように修正した：
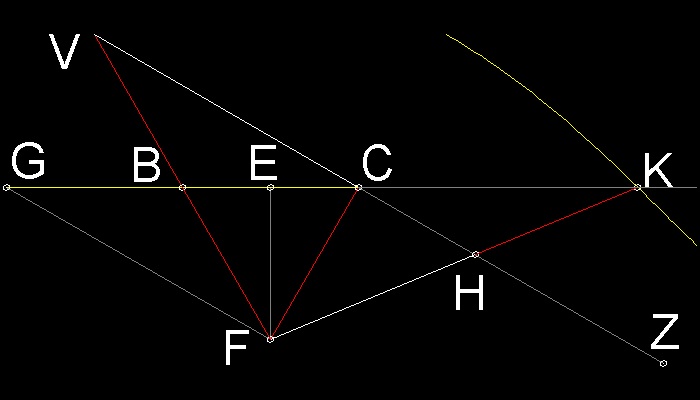
線分FB を引く。BV = BF (= CF = AD)となるように、その線分を点V へ伸ばす。
V と Cを結ぶ。
すると点V,C,H,Z は線分VZ上になる。
何故？-- ∠FCV は90度であることを示す。
ニコメデスのモデルの下の部分だけを取り出すと、次の図のようになる。


**************************** Nicomedes_modified.dwg **************************

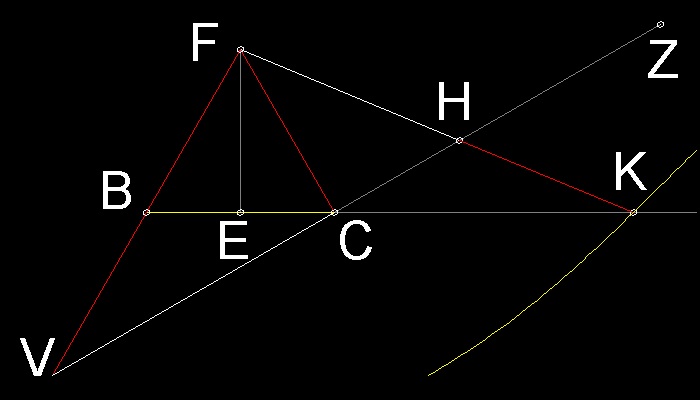
線分FG は、線分CH が線分VZ によって引かれるため、もう必要ない。
線分GF と点G を消去し、軸BC に関する全体図の鏡象を作ると、モデルは下の図のようになる。


*************************** Nicomedes_modified_a.dwg ************************

長さBC の定義で若干違う２つのモデルが Ref. 1 と 2 に示されている。

それらをここで選んだ理由は、両方とも大変おもしろい証明であるからである。

一般的な例 (Ref.2)

参照し易いように点の名前は(Ref.2)のものと一致するように変更する。
図中で、長さ AB = (k / 4) 、　 但し 0 < k < 8
線分CE は BA と平行に引く。
これの目的は、RS = 1 であるような点S を求めることである。
よって、 x = (k)1/3


*************************** Nicomedes_modified_b.dwg ************************
証明のまとめ (Ref.2) 

 
 B はCD の中点で AB は CE に平行であることから、CE = 2 AB = k / 2 
 また、三角形 ECR と ASR は相似であるから、(k/2) / CR = AS / 1　が得られる。
 AS = x　であれば、CR = k/(2x) 					(1) 
 ピタゴラスの定理を二度使って
 	CS2 = [1 + k /(2x)]2 = CM2 + MS2 = [CB2 - BM2] + MS2
			    = [12 - (k/8)2] + [x + (k/8)]2
 乗数順に x 項を並べ替えると、結果は次のような四次方程式となる。
 	4x4 + kx3 - kx - k2 = 0
 この方程式は次のように因数分解できる：
	(4x + k)(x3 - k) =  0

	(4x + k) >  0　であるから、 x3 - k = 0　

 従って、  x = (k)1/3 					(2)
 (2) を (1) に代入し
	y = CR = (1/2)k2/3				(3)
 ABC が正三角形である時 k = 4　
 そこで (2) と (3)　から、 BS( x ) と CR ( y ) は
		x = BS = (2)2/3
		y = CR = (2)1/3
 となる。
 この k = 4 の場合が、次のモデル(ref. 1)になる。

正三角形の場合 (Ref.1)

これはABC が正三角形の場合の例である。
次の図面では、AB = BC = CA = k
方法としては QP = k とする線分CP を引く。
よって､ CQ = k (2)1/3 で BP = y = k (2)2/3


* ************************** Nicomedes_modified_c.dwg ************************

このRef.1 では、前述の一般的な場合の証明ではなくて、非常におもしろい証明を行う。

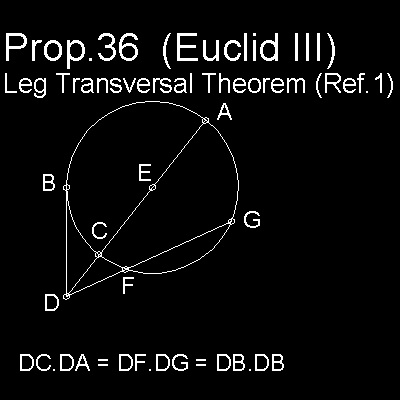
二つの有名な幾何学定理を用いる。一つはメネラウスの定理、もう一つはユークリッドの本(Book III)の中から定理３６。
後者（もしかして前者？？？）はRef.1の中で"the leg transversal theorem"と呼ばれる。
それらを次の図に示す。


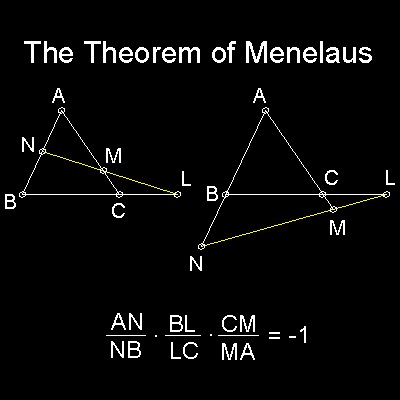
*********** Menelaus_theorem.dwg *********** ********** transversal_theorem.dwg **********

Ref.1 での証明。 

 
 準備:
   2k とk の間の二つの比例中項を求める方程式は
	2k/y = y/x = x/k
   であるから、三つの曲線がある。
	放物線-1	y2 = 2kx					(i)
	放物線-2	x2 = ky					(ii)
	双曲線	xy = 2k2					(iii)

   (1)（もしかして(i)？？？）と (ii) をまとめると、円の方程式ができる。
	円		x2 + y2 -2kx -ky = 0		(iv)

   (i) と (iv)の交点はデリアンの解を持つ。
   次の証明ではこのアイデアを用いる。
	
 (I)  メネラウスの定理を線分DBQ が横断する三角形ABC に適用すると
 	AD.CQ.BP = PQ.AB.CD または
		xy = 2k2							 (1)
 (II) 定理36 図では
	DF.DG = DC.DA = (DE - CE)(DE + CE) = DE2 - CE2	        	 (2)
      ここで、点C を中心とし半径k の円を考える。
	(2) は次のように表される
		PB.PA = PC2 - k2 または
		y (y + k) = (x + k)2 - k2 = x2 + 2kx 	  		 (3)

	
ここでの Ref.1 の証明は、(1)が双曲線を表し (3)は２つの放物線に等しい円方程式である、ということで留めておく。
故に(1) と (3)はデリアンの解である。

      さらに続けて解を求める。
	
      (1) を (3)に代入すると方程式は
		(2k + x)(x3 - 2k3) = 0
　　　(2k + x) >  0　であるから
		x3 - 2k3 = 0					 	 (4)
      従って、
		x = k (2)1/3

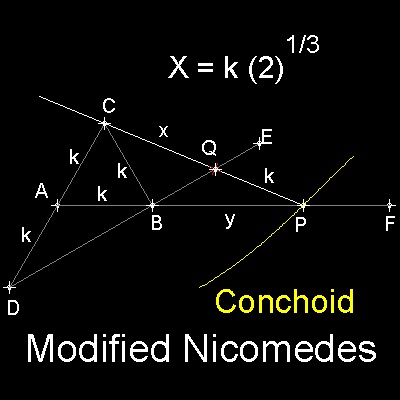
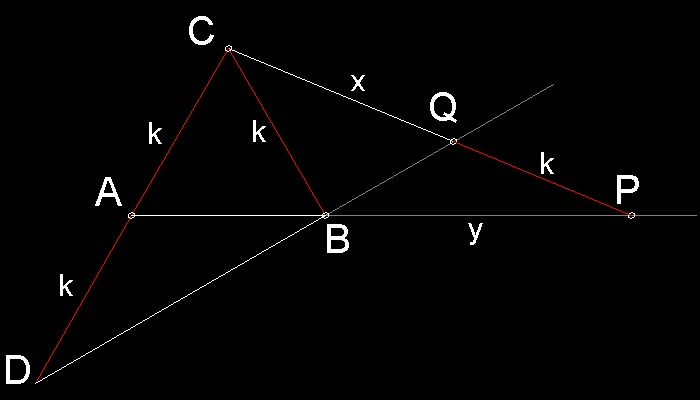
ABC は、辺の長さが k の正三角形である。
CA を伸ばし、A から k の距離に点D を与える。
D から B を通って点E へ線を引く。
A から B を通って点F へ線を引く。
点C を通り Q で線分BE に交差し、更に PQ = k であり、P で線分AF に交差する線を引く。

それで、 CQ = k (2)1/3　

点P を求めるためには
距離が k である位置に二つの印をした定規、またはコンコイド(Conchoid)曲線(C が 棒"pole", BE が 目盛り"rule", k が 距離"distance")を用いる。
******** modified_Nicomedes_desc.dwg *******

詳細は ニコメデス(Nicomedes) - Revisited の章で説明。

参考文献

1. Dorrie,Heinrich: "100 Great Problems of Elementary Mathematics",English translation, Dover, 1965.Original published in German in 1932

2. Martin,George E.: "Geometric Constructions",Undergraduate Texts in Mathematics,Springer Verlag,1997.

3. Descartes,Rene: "The Geometry of Rene Descartes",original in French and Latin, English Translation, Dover, 1925.

  ホームページの内容目次に戻る  古代ギリシャ数学の三大問題  デリアン問題

質問、問い合わせは 筆者 岩本 卓也宛てにお願いします。

Last Updated Nov 22, 2006

Copyright 2006 Takaya Iwamoto   All rights reserved.