チェバ(Tomasso
Ceva, 1648 - 1737) は1695年に「チェバのパントグラフ」(Ceva's
Pantograph)という三等分ツールを発表した。
パントグラフという名前は この器具が 平面曲線を拡大、縮小 トレースコピーするのにも使えるからである。
点Rを固定して、SB の間に Tをえらぶ。 RT がSO と交わる点をT'とする。
すると T を或る図形に沿って 動かすとき T' はその図形に相似な形状を描く。
パントマイム(pantomime)のパントと同じ語源で "真似する" と言う意味である。

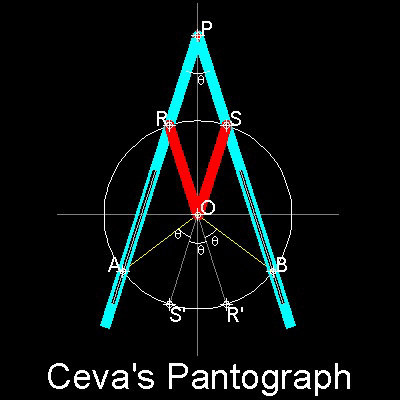
三等分の角を∠AOBとする。
点O は固定点で、
点P は線分PO に沿って移動する。
POは ∠AOB の二等分線である。
PR = PS = RO = SO となるように設定しておく。
点R と点S は円に沿って移動する。
線分PR の延長線が点A を通る時に
∠AOB は三等分される。
詳しくは
チェバのパントグラフ (Ceva's Pantograph) の章で説明。
*********** pantograph_desc.dwg
***********
アマドリは 1883 年に角を三等分するリンクに関する論文をイタリアで発行した。
アマドリのリンクを下図に示す。
アマドリのリンクに用いられる原理は、上記のチェバのパントグラフ
に適用したものと同じである。
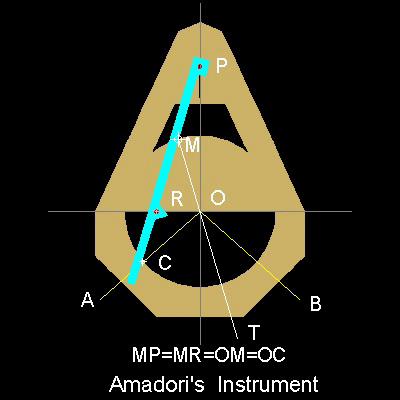
真っ直ぐな定規(PR)は、切り抜き円を持つ基板にくっ付いている。
点P は、点R が円の直径に沿って動くとき∠AOB の二等分線上
を動く。
よって∠AOB はPRの延長線 が点C を通る時に三等分される。
詳しくは
アマドリのリンク(Amadori's Link) の章で説明。
*********** Amadori_desc.dwg
***********
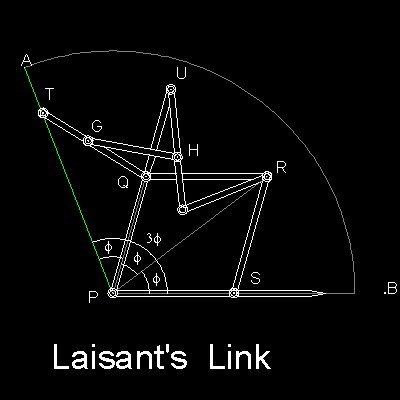
詳しくは
レイサントのリンク(Laisant's Links) の章で説明。
*********** Laisant_desc.dwg
***********
ケンぺ(Kempe,
Alfred Bray, 1849 - 1922) は1875年に角の三等分に使用できる大変ユニークなリンクを発表した。
[1]では ケンぺを素人(amateur)数学者と呼んでいるが 彼は数学界に大いなる貢献
をした人である。
ケンブリッジ大学を数学の優等生として卒業したその年に
"機構を使ってn 次方程式を解く一般的手法"
(A general method of solving equations of the n-th degree by mechanical means")と題する数学の論文を発表した。
しかし彼にとって 数学と音楽は単なる趣味でしかなく
本業は 教会関連の裁判における 法廷弁護士であった。
1874年の一月に ロンドンで シルベスター(Sylvester)の
"On recent discoveries in mechanical conversion of motion"
と題する講演を聴いて,円運動を直線運動に変換するリンク機構の研究を始め 1877年に
"どうしたら直線が引けるか?: リンク機構の講演"(How to draw a straight line: A lecture on linkages)
と題する連続講演を 王立研究所で行い 、同じ題名で 本も出版された。
余り知られていないが かれは "4 色 問題"(four color theorem)の証明の論文を1879年に
発表している。しかし
11年してからその論文に間違があることがわかった。
その100年後(1976年)に Kenneth Appel と Wolfgang Hakenによって
コンピューターを使った証明がなされたが
その基本的考えの二つは ケンペの論文によるものである。
ケンぺのリンクを下図に示す。
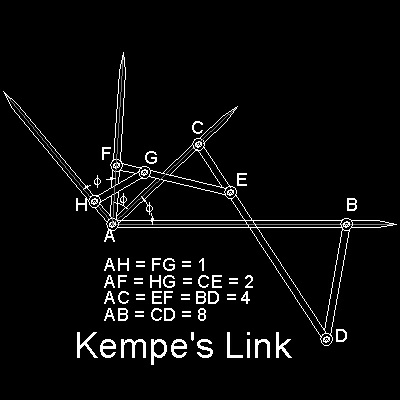
詳しくは
ケンぺのリンク(Kempe's Links) の章で説明。
*********** link_Kempe_desc.dwg
***********
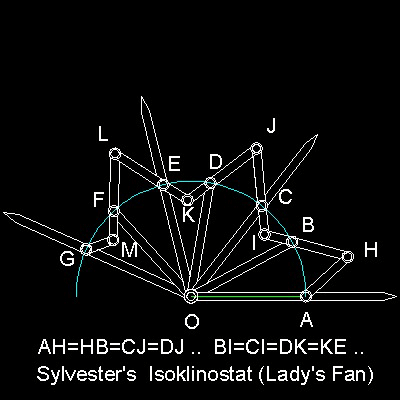
詳しくは
シルベスターの等傾斜装置(Sylvester's Isoklinostat) の章で説明。
*********** link_fan_desc.dwg
***********
アルキメデスの挿入法(Verging,Neusis)を適用する際、問題となるのは一点は 与えられた円周上、
もう一点は X-軸上に拘束したうえで その線が 三等分する角度を与える点の上に来るようにする操作が
必要であることである。
実際は目分量で適当にずらしながら最終位置を見つけることになる。
円運動を直線運動に変換するリンクをうまく利用すると
"X-軸上に拘束する" という条件を取り除くことができる。
すると 拘束条件は"円周上にある" こと一つになり
三等分する点に線を一致させることが容易になる。
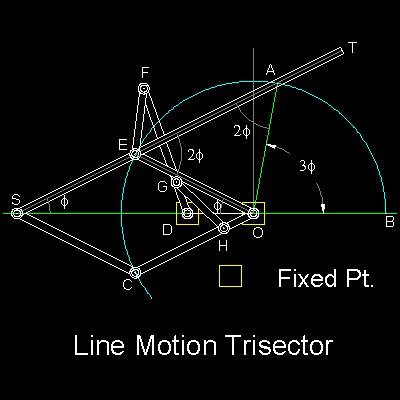
詳しくは
直線運動三等分器(Line Motion Trisector) の章で説明。
*********** link_motion_desc.dwg
***********
1. Yates,Robert Carl: "The Trisection problem",pp.31-46
質問、問い合わせは 筆者 岩本 卓也宛てにお願いします。
Last Updated Nov 22, 2006
Copyright 2006 Takaya Iwamoto All rights reserved.